Identification of COVID-19 spread mechanisms based on first-wave data, simulation models, and evolutionary algorithms

Abstract

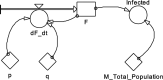
Background: The COVID-19 epidemic has shown that efficient prediction models are required, and the well-known SI, SIR, and SEIR models are not always capable of capturing the real dynamics. Modified models with novel structures could help identify unknown mechanisms of COVID-19 spread.

Objective: Our objective is to provide additional insights into the COVID-19 spread mechanisms based on different models' parameterization which was performed using evolutionary algorithms and the first-wave data.

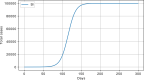
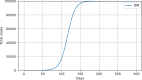
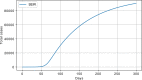
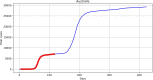
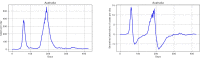
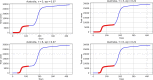
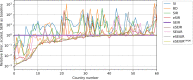
Methods: Data from the Our World in Data COVID-19 database was analysed, and several models-SI, SIR, SEIR, SEIUR, and Bass diffusion-and their variations were considered for the first wave of the COVID-19 pandemic. The models' parameters were tuned with differential evolution optimization method L-SHADE to find the best fit. The algorithm for the automatic identification of the first wave was developed, and the differential evolution was applied to model parameterization. The reproduction rates (R0) for the first wave were calculated for 61 countries based on the best fits.

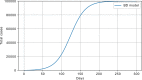
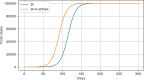
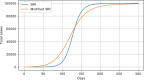
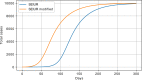
Results: The performed experiments showed that the Bass diffusion model-based modification could be superior compared to SI, SIR, SEIR and SEIUR due to the component responsible for spread from an external factor, which is not directly dependent on contact with infected individuals. The developed modified models containing this component were shown to perform better when fitting to the first-wave cumulative infections curve. In particular, the modified SEIR model was better fitted to the real-world data than the classical SEIR in 43 cases out of 61, based on Mann-Whitney U tests; the Bass diffusion model was better than SI for 57 countries. This showed the limitation of the classical models and indicated ways to improve them.

Conclusions: By using the modified models, the mechanism of infection spread, which is not directly dependent on contacts, was identified, which significantly influences the dynamics of the spread of COVID-19.

Fig 1. SI model response, cumulative number of infected; β = 0.1, S₀ = 100000, and I₀ = 1.

Fig 2. SIR model response, cumulative number of infected; β = 0.1, γ = 0.01, S₀ = 100000, and I₀ = 1.

Fig 3. SEIR model response, cumulative number of infected; β = 1, σ = 0.01, γ = 0.0005, S₀ = 100000, and I₀ = 1.

Fig 4. SEIUR model response, cumulative number of infected; β = 2, σ = 0.025, γ = 0.07, λ = 0.1, μ = 0.3, S₀ = 100000, and I₀ = 1.

Fig 5. BD model, first variant.

Fig 6. BD model, second variant.

Fig 7. Bass diffusion model response; p = 10⁻⁴, q = 0.05, S₀ = 100000, and I₀ = 0.

Fig 8. SI vs eSI model response; β = 0.1, θ = 1∙10⁻⁵, S₀ = 100000, and I₀ = 1.

Fig 9. SIR vs. eSIR model response; S₀ = 100000 and I₀ = 1.

Fig 10. SEIR vs. eSEIR model response; S₀ = 100000 and I₀ = 1.

Fig 11. SEIUR vs. eSEIUR model response; S₀ = 100000 and I₀ = 1.

Fig 12. Example of two waves of infections; the first wave is highlighted.

Fig 13. Example of number of cases per day and calculated smoothed derivative.

Fig 14. Influence of first wave search heuristic parameters on the result.

Fig 15. Scaled relative error values of tested models, ordered by eSEIR.

Fig 16. Values of β parameter, results from all runs on all countries.

Fig 17. Example of fitting all models to real data on Saudi Arabia.