Unified Principal Component Analysis for Sparse and Dense Functional Data under Spatial Dependency

Abstract

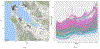
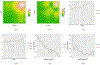
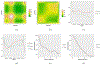
We consider spatially dependent functional data collected under a geostatistics setting, where locations are sampled from a spatial point process. The functional response is the sum of a spatially dependent functional effect and a spatially independent functional nugget effect. Observations on each function are made on discrete time points and contaminated with measurement errors. Under the assumption of spatial stationarity and isotropy, we propose a tensor product spline estimator for the spatio-temporal covariance function. When a coregionalization covariance structure is further assumed, we propose a new functional principal component analysis method that borrows information from neighboring functions. The proposed method also generates nonparametric estimators for the spatial covariance functions, which can be used for functional kriging. Under a unified framework for sparse and dense functional data, infill and increasing domain asymptotic paradigms, we develop the asymptotic convergence rates for the proposed estimators. Advantages of the proposed approach are demonstrated through simulation studies and two real data applications representing sparse and dense functional data, respectively.

Keywords: covariance estimation; dimension deduction; infill asymptotics; nugget effect; spatio-temporal; tensor product splines.

Fig. 1

London house price data. (a) Locations of houses in the Greater London Area; (b) trajectories of the house prices and the estimated mean function (dashed line).

Fig. 2

(a) The locations of the 234 neighborhoods in the San Francisco Bay Area; (b) trajectories of the home price-to-rent ratios, observed monthly from October 2010 to August 2018 in the 234 neighborhoods.

Fig. 3

Estimation results of sFPCA under Scenario A. Panels (a) - (h) contain summaries of the functional estimators, as described in the labels. In each panel, the solid line is the true function; the dashed line is the mean of the functional estimator; and the shaded area illustrates the bands of pointwise 5% and 95% percentiles. Panel (i) contains the boxplots of ${\widehat{\varpi }}_1$, ${\widehat{\varpi }}_2$, ${\widehat{\varpi }}_3$, ${\widehat{\omega }}_{\text{nug},1}$, and ${\widehat{\omega }}_{\text{nug},2}$.

Fig. 4

Estimation results of iFPCA under Scenario A. In each panel, the solid line is the true function; the dashed line is the mean of the functional estimator; and the shaded area illustrates the bands of pointwise 5% and 95% percentiles.

Fig. 5

Results on the London housing price data: (a) contour plot of $\widehat{\Omega }(t_1,t_2)$; (b) contour plot of $\widehat{\Lambda }(t_1,t_2)$, covariance of the functional nugget effect; (c) the first two eigenfunctions of $\widehat{\Omega }(\cdot ,\cdot )$; (d) the first three eigenfunctions of $\widehat{\Lambda }(\cdot ,\cdot )$; (e) spatial correlation function ${\widehat{\rho }}_1(\cdot )$ and its positive semi-definite adjustment ${\tilde{\rho }}_1(\cdot )$; (f) ${\widehat{\rho }}_2(\cdot )$ and ${\tilde{\rho }}_2(\cdot )$.

Fig. 6

Results on the Zillow real estate data: (a) contour plot of $\widehat{\Omega }(t_1,t_2)$; (b) contour plot of $\widehat{\Lambda }(t_1,t_2)$, covariance function of the functional nugget effect; (c) the first two eigenfunctions (d) the first three eigenfunctions of $\widehat{\Lambda }(\cdot ,\cdot )$ (e) the estimated spatial correlation function ${\widehat{\rho }}_1(\cdot )$ and its positive semi-definite adjustment ${\tilde{\rho }}_1(\cdot )$; (f) ${\widehat{\rho }}_2(\cdot )$ and ${\tilde{\rho }}_2(\cdot )$.