Nonnegative spatial factorization applied to spatial genomics
- PMID: 36587187
- PMCID: PMC9911348
- DOI: 10.1038/s41592-022-01687-w
Nonnegative spatial factorization applied to spatial genomics
Abstract
Nonnegative matrix factorization (NMF) is widely used to analyze high-dimensional count data because, in contrast to real-valued alternatives such as factor analysis, it produces an interpretable parts-based representation. However, in applications such as spatial transcriptomics, NMF fails to incorporate known structure between observations. Here, we present nonnegative spatial factorization (NSF), a spatially-aware probabilistic dimension reduction model based on transformed Gaussian processes that naturally encourages sparsity and scales to tens of thousands of observations. NSF recovers ground truth factors more accurately than real-valued alternatives such as MEFISTO in simulations, and has lower out-of-sample prediction error than probabilistic NMF on three spatial transcriptomics datasets from mouse brain and liver. Since not all patterns of gene expression have spatial correlations, we also propose a hybrid extension of NSF that combines spatial and nonspatial components, enabling quantification of spatial importance for both observations and features. A TensorFlow implementation of NSF is available from https://github.com/willtownes/nsf-paper .
© 2022. The Author(s).
Conflict of interest statement
B.E.E. is on the SAB for Creyon Bio, ArrePath and Freenome. B. E. E. consults for Neumora and Cellarity. The remaining author declares no competing interests.
Figures





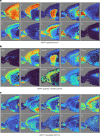

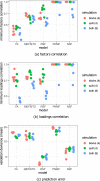
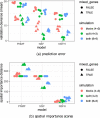
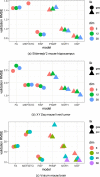





Comment in
-
Parts-based decomposition of spatial genomics data finds distinct tissue regions.Nat Methods. 2023 Feb;20(2):187-188. doi: 10.1038/s41592-022-01725-7. Nat Methods. 2023. PMID: 36611125 Free PMC article.
References
-
- Editors. Method of the year 2020: spatially resolved transcriptomics. Nat. Methods18, 1 (2021). - PubMed
-
- Bartholomew, D. J., Knott, M. & Moustaki, I. Latent Variable Models and Factor Analysis: A Unified Approach (John Wiley & Sons, 2011).
-
- Rasmussen, C. E. & Williams, C. K. I. Gaussian Processes for Machine Learning (MIT Press, 2005).
-
- Banerjee, S., Carlin, B. P. & Gelfand, A. E. Hierarchical Modeling and Analysis for Spatial Data (CRC Press, 2014).
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

