A cognitive process modeling framework for the ABCD study stop-signal task

Abstract

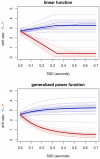
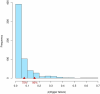
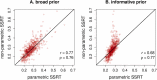
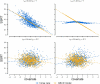
The Adolescent Brain Cognitive Development (ABCD) Study is a longitudinal neuroimaging study of unprecedented scale that is in the process of following over 11,000 youth from middle childhood though age 20. However, a design feature of the study's stop-signal task violates "context independence", an assumption critical to current non-parametric methods for estimating stop-signal reaction time (SSRT), a key measure of inhibitory ability in the study. This has led some experts to call for the task to be changed and for previously collected data to be used with caution. We present a cognitive process modeling framework, the RDEX-ABCD model, that provides a parsimonious explanation for the impact of this design feature on "go" stimulus processing and successfully accounts for key behavioral trends in the ABCD data. Simulation studies using this model suggest that failing to account for the context independence violations in the ABCD design can lead to erroneous inferences in several realistic scenarios. However, we demonstrate that RDEX-ABCD effectively addresses these violations and can be used to accurately measure SSRT along with an array of additional mechanistic parameters of interest (e.g., attention to the stop signal, cognitive efficiency), advancing investigators' ability to draw valid and nuanced inferences from ABCD data. AVAILABILITY OF DATA AND MATERIALS: Data from the ABCD Study are available through the NIH Data Archive (NDA): nda.nih.gov/abcd. Code for all analyses featured in this study is openly available on the Open Science Framework (OSF): osf.io/2h8a7/.

Keywords: Bayesian cognitive modeling; Evidence accumulation; Inhibition; Parameter recovery; Trigger failure.

Fig. 1

Models of the stop signal task. (A) The original independent race model, consisting of a race between the go and stop processes while accounting for the stop signal delay (SSD). The stop process wins the first race shown, resulting in a successful inhibition, while the go process wins the second race, resulting in an incorrect “signal response”. (B) The Bayesian parametric estimation of stop-signal reaction time distributions (BEESTS: Matzke et al., 2013) framework models the entire distributions of go and stop process finishing times as ex-Gaussian (i.e., right-skewed normal) distributions. (C) An example of “trigger failure” leading to a signal response by preventing the stop process from entering the race. (D) The racing-diffusion (Logan et al., 2014) model’s explanation of an example stop trial; accumulators gather noisy evidence over time for the choices matching and mismatching the go stimulus as well as for the stop process. In this case, the accumulator for the matching go choice process reaches threshold before the stop process accumulator, causing a signal response to be made. (E) The “hybrid” racing-diffusion ex-Gaussian (RDEX) model framework (Tanis et al., 2022) that combines an evidence-accumulation model of the go process with an ex-Gaussian model of stop process finishing times. Go RTs result from a race between accumulators that gather noisy evidence for the choices matching and mismatching the stimulus (in this example, a right-facing arrow) at average rates of v₊ and v_-, respectively, until one accumulator crosses a response threshold. Stop process finishing times are drawn from a Gaussian distribution specified by mean (μ) and standard deviation (σ) parameters and convolved with an exponential distribution with mean τ. (F) The RDEX-ABCD model’s explanation for the impact of context independence violations on stop trials. Evidence signals for the matching and mismatching accumulators on stop trials of a given SSD are the sum of a processing speed component that drives evidence accumulation for both choices equally and a discrimination component that favors the choice matching the presented stimulus. Processing speed is determined by parameter v₀ and is identical across all SSDs. The discrimination component is completely absent (equal to 0) at a 0 s SSD, as the choice stimulus is not presented, but increases linearly at the same rate g for both matching and mismatching components until they reach the level of v₊ and v_-on go trials. Therefore, the match and mismatch rates are identical on 0 s SSD trials and gradually move apart from each other at longer SSDs until they become equal to their go trial levels.

Fig. 2

Posterior predictive plots showing the RDEX-ABCD model and comparison models’ median predictions (red line) and 99% credible intervals (CIs) of predictions (red shading) for key trends in the ABCD stop-signal task data, overlayed with empirical values (dots). All models were fit with informative priors. Choice accuracy for signal-respond trials is binned by SSD, showing the hallmark effect of the ABCD task’s violation of context independence: the systematic increase in choice accuracy with go stimulus presentation times. For the “relative” inhibition functions, SSDs are binned at the individual level to account for individual differences in performance. For the “absolute” inhibition functions and plots of median signal-respond response time (RT) by SSD, SSD bins are created by collapsing SSDs for observed trials across the whole group.

Fig. 3

Empirical growth patterns of matching (blue lines increasing from SSD = 0) and mismatching (red lines decreasing from SSD = 0) “go” process accumulator rates by stop-signal delay (SSD) for the sample average parameter estimates (thick lines) and for parameter estimates from 20 randomly drawn participants (thin lines) to illustrate individual variability.

Fig. 4

Histogram of individual-level estimates (posterior medians) for the probability of trigger failure in the 600-person ABCD subsample. Red triangles denote the 75th and 90th percentiles.

Fig. 5

Comparison of non-parametric SSRT estimates with parametric estimates obtained from RDEX-ABCD, both when the model is estimated with broad, uninformative priors (A) and when it is estimated with narrower priors informed by a hierarchical model fit (B). The black line represents where dots would fall along if the relation between the two sets of estimates was perfect. Correlation coefficients for each relation, including both Pearson’s r and Spearman’s ρ, are displayed in the bottom right corner of each plot.

Fig. 6

A demonstration of the influence of processing speed and perceptual growth rate on the non-parametric SSRT of two individuals based on 15,000 simulated “go” and 5000 simulated “stop” trials each. Persons A and B (left) have a similar level of speed as indicated by the crosses, but a differing SSRT. When speed is varied, the estimated non-parametric SSRT is affected even though this change should not lead to a different SSRT. Similarly, persons A and C (right) have a similar level of perceptual growth rate, and varying this rate also affects the estimated non-parametric SSRT. Both cases result in two regions leading to qualitatively different conclusions. In reality, person A has a higher SSRT than persons B and C, and this true parametric SSRT (horizontal lines) is independent of both speed and perceptual growth rate. Note that with the large number of trials in these simulations RDEX-ABCD parametric SSRTs are essentially perfect, and so the horizontal lines correspond to the true data generating values.

Fig. 7

Demonstrations of covariate confounds influencing non-parametric SSRT estimates in a simulated correlational analysis. A covariate was created that has a relation with both processing speed (v₀) and SSRT (through the μ parameter) for 900 simulated participants. The scatterplots display the observed relations between SSRT and the covariate when non-parametric methods (blue) versus the parametric RDEX-ABCD model (orange) are alternately used to estimate SSRT.

Fig. 8

Results from the parameter recovery study in which informed priors were used to estimate parameters (both the initial parameter values estimated from empirical data and the parameter values recovered from simulated data). Scatterplots illustrate the relations between the simulated (“sim.”) and recovered (“rec.”) parameter values as compared to the diagonal solid line indicating perfect recovery. Numbers above each plot report the correlation coefficient (r) for each relation and the posterior coverage proportions (c) for each parameter, which indicate the proportion of data-generating parameter values that fall within the 95 % posterior credible interval for the parameters recovered from the generated data.

Fig. 9

Results from the parameter recovery study in which broad priors were used to estimate parameters (both the initial parameter values estimated from empirical data and the parameter values recovered from simulated data). Scatterplots illustrate the relations between the simulated (“sim.”) and recovered (“rec.”) parameter values as compared to the solid diagonal line indicating perfect recovery. Numbers above each plot report the correlation coefficient (r) for each relation and the posterior coverage proportions (c) for each parameter, which indicate the proportion of data-generating parameter values that fall within the 95 % posterior credible interval for the parameters recovered from the generated data.