Gaussian Curvature Effects on Graphene Quantum Dots

Abstract

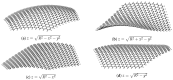
In the last few years, much attention has been paid to the exotic properties that graphene nanostructures exhibit, especially those emerging upon deforming the material. Here we present a study of the mechanical and electronic properties of bent hexagonal graphene quantum dots employing density functional theory. We explore three different kinds of surfaces with Gaussian curvature exhibiting different shapes-spherical, cylindrical, and one-sheet hyperboloid-used to bend the material, and several boundary conditions regarding what atoms are forced to lay on the chosen surface. In each case, we study the curvature energy and two quantum regeneration times (classic and revival) for different values of the curvature radius. A strong correlation between Gaussian curvature and these regeneration times is found, and a special divergence is observed for the revival time for the hyperboloid case, probably related to the pseudo-magnetic field generated by this curvature being capable of causing a phase transition.

Keywords: DFT; Gaussian curvature; graphene; phase transition; pseudo-magnetic field; quantum revival.

Figure 1

Hexagonal, flat graphene quantum dot used as a starting point for deformation. Image generated with Gaussview 6 [91].

Figure 2

The four different geometries considered in this study for the graphene dot with $R=50$ Å and their respective equations: (a) sphere; (b) one-sheet hyperboloid; (c) x-cylinder; (d); y-cylinder. Images generated with GaussView 6 [91].

Figure 3

Boundary conditions’ effects on the optimized geometries of an initially spherical quantum dot with $R=40$ Å. Images generated with Gaussview 6 [91]. (a) Fixed surface; (b) fixed edges; (c) fixed vertices.

Figure 4

Curvature energy vs. $1/R^2$ for all four ideal geometries—all atoms forced to lay on the surface—with the flat dot taken as energy origin. Both cylindrical cases give almost identical energies.

Figure 5

Curvature energy vs. $1/R^2$ plots for all geometries, with the flat dot taken as energy origin.

Figure 6

View of ${\left|A\left(t\right)\right|}^2$ as a function of t for a spherical dot with $R=100$ Å. Analytical values of both regeneration times are shown with dotted lines (orange for classical time, yellow for revival time).

Figure 7

Classical time plots as functions of $1/R^2$ for all four ideal geometries, with numerical values as markers and analytical ones as dotted lines. Both cylinders show near perfect coincidence.

Figure 8

Classical time as a function of $1/R^2$ for different boundary conditions within each geometry, with numerical values as points and analytical ones as dotted lines.

Figure 9

Revival time as a function of $1/R^2$ for all four ideal geometries, with numerical values as points and analytical ones as dotted lines.

Figure 10

Revival time as a function of $1/R^2$ for different boundary conditions within each geometry, with the numerical values as markers and the analytical ones as dotted lines.