The Ewald sphere/focus gradient does not limit the resolution of cryoEM reconstructions

Abstract

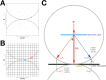
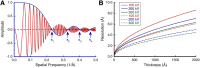
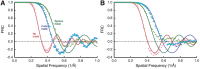
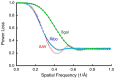
In our quest to solve biomolecular structures to higher resolutions in cryoEM, care must be taken to deal with all aspects of image formation in the electron microscope. One of these is the Ewald sphere/focus gradient that derives from the scattering geometry in the microscope and its implications for recovering high resolution and handedness information. While several methods to deal with it has been proposed and implemented, there are still questions as to the correct approach. At the high acceleration voltages used for cryoEM, the traditional projection approximation that ignores the Ewald sphere breaks down around 2-3 Å and with large particles. This is likely not crucial for most biologically interesting molecules, but is required to understand detail about catalytic events, molecular orbitals, orientation of bound water molecules, etc. Through simulation I show that integration along the Ewald spheres in frequency space during reconstruction, the "simple insertion method" is adequate to reach resolutions to the Nyquist frequency. Both theory and simulations indicate that the handedness information encoded in such phases is irretrievably lost in the formation of real space images. The conclusion is that correct reconstruction along the Ewald spheres avoids the limitations of the projection approximation.

Keywords: AAV, Adeno-associated virus; CTF, Contrast transfer function; CryoEM, Cryo-electron microscopy; Electron microscopy; FRC, Fourier ring correlation; FSC, Fourier shell correlation; Handedness; Projection approximation; Single particle analysis.

Graphical abstract

Fig. 1

(A) The Ewald sphere (gray circles) superimposed on a crystal lattice in frequency space. The circles indicate reflections that intersect with the Ewald sphere and would appear in a diffraction image, with the blue circle on the central section plane, while the red circle is in the next layer. (B) The corresponding layout of frequency space voxels of a single particle map where the Ewald sphere intersects with voxels such as the blue one on the central section, progressing towards adjacent layers such as the red voxel. (C) Illustration of the definitions of the different terms describing the Ewald spheres, including the scattering angle, $\theta$, the distance on the back focal plane corresponding to the spatial frequency, s, and the difference between the back focal plane and the Ewald sphere in the direction of the beam, w_ew. Also indicated are the structure factors for the upper (F_u) and lower (F_l) Ewald spheres, and the left (F_L) and right (F_R) scattered electrons.

Fig. 2

(A) The sinc function (blue curve) follows the envelope of the CTF (red curve) simulated at 100 kV for a defocus gradient from 1 µm to 1.1 µm (1000 Å thickness). Even if the CTF is corrected to account for the contrast reversals in the red curve, the contrast reversals at the nodes in the sinc envelope remains (arrows). (B) Resolutions where the influence of the Ewald sphere/defocus gradient becomes important (solid curves) and the resolution limits at the first node (s₁) of the sinc function (dashed curves).

Fig. 3

(A) Flow chart illustrating the calculation of the central section (FS_cs) or the Ewald spheres (FS_ew) in frequency space. The Ewald spheres can also be directly calculated from the atomic coordinates by imposing a focal shift on each z coordinate (FS_Δf). The frequency space central section and Ewald sphere are then back transformed to produce the real space projections (RS_cs and RS_ew). The difference image in the bottom center (RS_cs-RS_ew) emphasizes the subtle difference in the high frequency contributions. (B) The FRC between the central section (FS_cs) and the Ewald sphere (FS_ew) in frequency space follows a sinc function (red circles) with the first node at 2 Å for the AAV test case (acceleration voltage = 100 kV, defocus Δf = 1 µm). The FRC after transforming both images to real space (RS_cs vs RS_ew) gives better correlation (blue squares). The FRC between the Ewald sphere and the Ewald sphere projection transformed back to frequency space (green diamonds) indicates that the loss on the conversion to real space is only partial. Fitted equations: ${\mathit{FRC}}_{\mathit{red}}(s)=sinc(\pi 4.0s^2)$; ${\mathit{FRC}}_{\mathit{green}}\left(s\right)=0.26sinc\left(\pi 8.0s^2\right)+0.74$; ${\mathit{FRC}}_{\mathit{blue}}\left(s\right)={\mathit{FRC}}_{\mathit{red}}(s)/{\mathit{FRC}}_{\mathit{green}}\left(s\right)$. (C) The FRC between the central section and the Ewald sphere (red discs) is the same as for the focus gradient (FS_Δf) imposed on the central section (blue squares).

Fig. 4

The influence of effective thickness on comparisons between projection images calculated from the central section and Ewald sphere. (A) Projection images at 100 kV from a volume of 1000³ with gaussian noise, sampled at 0.5 Å/voxel. The red curve is for the whole volume without masking, while the blue curve is after applying a rectangular mask of 500³ voxels, and the green curve is after applying a spherical mask of radius 250 voxels. The sinc function fits indicate effective thicknesses of 500 Å, 250 Å and 189 Å respectively. The corresponding first nodes (at the dashed line) are at resolutions of 3.05 Å, 2.15 Å and 1.87 Å, respectively. (B) Projection images calculated from atomic coordinates of a non-spherical particle. The coordinates of the two copies of a 70S ribosome (PDB accession number 1VY4) were used to calculate projections from orthogonal views at 100 kV. The curves are sinc functions for thicknesses of ∼332 Å (red), ∼215 Å (green) and ∼162 Å (blue), compared to the longest (∼440 Å) and shortest (∼200 Å) axes of the particle.

Fig. 5

Reconstructions from simulated projection images calculated from central sections or the Ewald sphere, compared by FSC (A,C,E) and assessed by their radial power spectra (B,D,F), for the cases of AAV (A,B), the ribosome dimer (C,D) and β-galactosidase (E,F). Reconstruction from Ewald sphere projections along the Ewald spheres in frequency space recovers phase information to high resolution (A,C,E: ew2ew, red discs). Reconstruction from central sections along the Ewald spheres (A,C,E: cs2ew, green diamonds) or reconstruction from Ewald sphere projections along the central sections (A,C,E: ew2cs, blue squares) severely suppresses phase information at high resolution. Radial power spectra of the reconstructions coincide at low resolution (B,D,F). Using the central section-to-central section reconstruction (cs2cs, black circles) as reference, the spectral power for the other reconstructions is suppressed.

Fig. 6

Loss of power in the reconstructions using the simple insertion method. The curves indicate the ratios of the ew2ew reconstruction powers to the corresponding cs2cs reconstruction in Fig. 5.