Reconstruction of 3D density from solution scattering
- PMID: 36641207
- PMCID: PMC10246859
- DOI: 10.1016/bs.mie.2022.09.018
Reconstruction of 3D density from solution scattering
Abstract
Ab initio modeling methods have proven to be powerful means of interpreting solution scattering data. In the absence of atomic models, or complementary to them, ab initio modeling approaches can be used for generating low-resolution particle envelopes using only solution scattering profiles. Recently, a new ab initio reconstruction algorithm has been introduced to the scientific community, called DENSS. DENSS is unique among ab initio modeling algorithms in that it solves the inverse scattering problem, i.e., the 1D scattering intensities are directly used to determine the 3D particle density. The reconstruction of particle density has several advantages over conventional uniform density modeling approaches, including the ability to reconstruct a much wider range of particle types and the ability to visualize low-resolution density fluctuations inside the particle envelope. In this chapter we will discuss the theory behind this new approach, how to use DENSS, and how to interpret the results. Several examples with experimental and simulated data will be provided.
Keywords: Ab initio; Density; Imaging; Modeling; Phase retrieval; Small angle scattering.
Copyright © 2023 Elsevier Inc. All rights reserved.
Figures



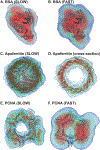
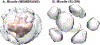
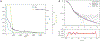



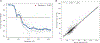

Similar articles
-
DENSS-multiple: A structure reconstruction method using contrast variation of small-angle neutron scattering based on the DENSS algorithm.BBA Adv. 2022 Nov 8;2:100063. doi: 10.1016/j.bbadva.2022.100063. eCollection 2022. BBA Adv. 2022. PMID: 37082592 Free PMC article.
-
Ab initio electron density determination directly from solution scattering data.Nat Methods. 2018 Mar;15(3):191-193. doi: 10.1038/nmeth.4581. Epub 2018 Jan 29. Nat Methods. 2018. PMID: 29377013
-
Fitting high-resolution electron density maps from atomic models to solution scattering data.Biophys J. 2023 Dec 5;122(23):4567-4581. doi: 10.1016/j.bpj.2023.10.034. Epub 2023 Nov 2. Biophys J. 2023. PMID: 37924208 Free PMC article.
-
Application of SAXS for the Structural Characterization of IDPs.Adv Exp Med Biol. 2015;870:261-89. doi: 10.1007/978-3-319-20164-1_8. Adv Exp Med Biol. 2015. PMID: 26387105 Review.
-
Structural analysis of intrinsically disordered proteins by small-angle X-ray scattering.Mol Biosyst. 2012 Jan;8(1):151-67. doi: 10.1039/c1mb05275f. Epub 2011 Sep 22. Mol Biosyst. 2012. PMID: 21947276 Review.
Cited by
-
Crystal structure of coagulation factor XII N-terminal domains 1-5.Acta Crystallogr D Struct Biol. 2025 Jul 1;81(Pt 7):380-393. doi: 10.1107/S2059798325005297. Epub 2025 Jun 27. Acta Crystallogr D Struct Biol. 2025. PMID: 40576968 Free PMC article.
-
Structural insights into redox signal transduction mechanisms in the control of nitrogen fixation by the NifLA system.Proc Natl Acad Sci U S A. 2023 Jul 25;120(30):e2302732120. doi: 10.1073/pnas.2302732120. Epub 2023 Jul 17. Proc Natl Acad Sci U S A. 2023. PMID: 37459513 Free PMC article.
-
Temporal ghost imaging for pump-probe X-ray solution scattering.Acta Crystallogr A Found Adv. 2025 Sep 1;81(Pt 5):371-380. doi: 10.1107/S2053273325004243. Epub 2025 Jul 7. Acta Crystallogr A Found Adv. 2025. PMID: 40620178 Free PMC article.
-
Analyzing aptamer structure and interactions: in silico modelling and instrumental methods.Biophys Rev. 2024 Nov 20;16(6):685-700. doi: 10.1007/s12551-024-01252-z. eCollection 2024 Dec. Biophys Rev. 2024. PMID: 39830127 Review.
References
-
- Bernadó P, Mylonas E, Petoukhov MV, Blackledge M, & Svergun DI (2007). Structural characterization of flexible proteins using small-angle X-ray scattering. Journal of the American Chemical Society, 129(17), 5656–5664. - PubMed
-
- Beyett TS, Fraley AE, Labudde E, Patra D, Coleman RC, Eguchi A, et al. (2019). Perturbation of the interactions of calmodulin with GRK5 using a natural product chemical probe. Proceedings of the National Academy of Sciences of the United States of America, 116(32), 15895–15900. 10.1073/pnas.1818547116. - DOI - PMC - PubMed
-
- Brown PJ, Fox AG, Maslen EN, O’Keefe MA, & Willis BTM (2006). Intensity of diffracted intensities. International Tables for Crystallography, 554–595.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

