Bayesian design for minimizing prediction uncertainty in bivariate spatial responses with applications to air quality monitoring

Abstract

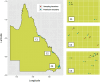
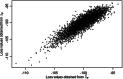
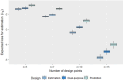
Model-based geostatistical design involves the selection of locations to collect data to minimize an expected loss function over a set of all possible locations. The loss function is specified to reflect the aim of data collection, which, for geostatistical studies, could be to minimize the prediction uncertainty at unobserved locations. In this paper, we propose a new approach to design such studies via a loss function derived through considering the entropy about the model predictions and the parameters of the model. The approach includes a multivariate extension to generalized linear spatial models, and thus can be used to design experiments with more than one response. Unfortunately, evaluating our proposed loss function is computationally expensive so we provide an approximation such that our approach can be adopted to design realistically sized geostatistical studies. This is demonstrated through a simulated study and through designing an air quality monitoring program in Queensland, Australia. The results show that our designs remain highly efficient in achieving each experimental objective individually, providing an ideal compromise between the two objectives. Accordingly, we advocate that our approach could be adopted more generally in model-based geostatistical design.

Keywords: bivariate response models; copula models; entropy; generalized linear spatial models; spatial dependence.

FIGURE 1

The locations of the selected air quality monitoring stations

FIGURE 2

The relationship between the loss values obtained from ${\widehat{\lambda }}_P(\mathit{d},\mathbf{y})$ and ${\stackrel{\sim }{\lambda }}_P(\mathit{d},\mathbf{y})$ for 100 randomly generated designs under moderate spatial dependence from Example 1

FIGURE 3

The optimal designs selected from each loss function (n = 5)

FIGURE 4

The optimal designs selected from each loss function (n = 10)

FIGURE 5

Boxplots of the values of the parameter estimation expected loss function for the estimation, prediction, and dual‐purpose designs from Example 1 based on 100 simulations

FIGURE 6

Boxplots of the values of the prediction expected loss function for the estimation, prediction, and dual‐purpose designs from Example 1 based on 100 simulations

FIGURE 7

The relationship between the loss values obtained from ${\widehat{\lambda }}_P(\mathit{d},\mathbf{y})$ and ${\stackrel{\sim }{\lambda }}_P(\mathit{d},\mathbf{y})$ for 100 randomly generated designs from Example 2

FIGURE 8

The optimal monitoring stations selected from each loss function

FIGURE 9

Boxplots of the values of the parameter estimation expected loss function for the estimation, prediction, and dual‐purpose designs from Example 2 based on 50 simulations

FIGURE 10

Boxplots of the values of the prediction expected loss function for the estimation, prediction, and dual‐purpose designs from Example 2 based on 50 simulations