Coherent correlation imaging for resolving fluctuating states of matter

Abstract

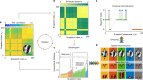
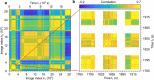
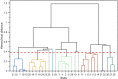
Fluctuations and stochastic transitions are ubiquitous in nanometre-scale systems, especially in the presence of disorder. However, their direct observation has so far been impeded by a seemingly fundamental, signal-limited compromise between spatial and temporal resolution. Here we develop coherent correlation imaging (CCI) to overcome this dilemma. Our method begins by classifying recorded camera frames in Fourier space. Contrast and spatial resolution emerge by averaging selectively over same-state frames. Temporal resolution down to the acquisition time of a single frame arises independently from an exceptionally low misclassification rate, which we achieve by combining a correlation-based similarity metric^1,2 with a modified, iterative hierarchical clustering algorithm^3,4. We apply CCI to study previously inaccessible magnetic fluctuations in a highly degenerate magnetic stripe domain state with nanometre-scale resolution. We uncover an intricate network of transitions between more than 30 discrete states. Our spatiotemporal data enable us to reconstruct the pinning energy landscape and to thereby explain the dynamics observed on a microscopic level. CCI massively expands the potential of emerging high-coherence X-ray sources and paves the way for addressing large fundamental questions such as the contribution of pinning^5-8 and topology^9-12 in phase transitions and the role of spin and charge order fluctuations in high-temperature superconductivity^13,14.

Fig. 1. Conventional imaging of fluctuating magnetic domains.

a, Example images of the thermally evolving magnetic maze domain states at 310 K. Each image has been reconstructed by Fourier-transform holography from scattering data sequentially averaged over the indicated time intervals. High-contrast regions indicate stationary behaviour of the local out-of-plane magnetization m_z, and grey features correspond to unresolved dynamics during the averaging period. b, Example images reconstructed from averages of fewer frames. c–f, Disentangled magnetic domain states corresponding to the time interval of b. The domain states were identified and reconstructed using CCI. Scale bar, 500 nm.

Fig. 2. Principle of time-resolved coherent correlation imaging.

Top, sequence of camera frames showing Fourier-space coherent scattering patterns. Coherent correlation imaging classifies scattering frames by their underlying domain state, as indicated by the colours. Bottom, real-space images reconstructed from an informed average of same-state frames. Scale bar, 500 nm.

Fig. 3. Illustration of the CCI algorithm.

a, Pair correlation map of an exemplary set of 250 camera snapshots. The inset shows the magnetic image reconstructed from the sequential average of all 250 snapshots. b, Similarity distance derived from the normalized pair correlation of the pattern in a. c, Dendrogram calculated from b by an agglomerative, hierarchical clustering algorithm. Natural divisions are identified by exceptionally large inconsistencies between the vertical step size and the standard deviation of lower-level links, as indicated by the colour. The complete separation into the clusters in d is performed iteratively as indicated. See Methods for details. d, Spatially resolved set of domain configurations reconstructed from an informed average of all snapshots of each cluster. e, Reconstructed temporal evolution of states, as obtained by grouping domain configurations from d, that is, by grouping the internal modes A₁ and A₂. Dashed lines indicate times without data points. Scale bars, 500 nm.

Fig. 4. CCI resolved dynamics of the fluctuating domain network.

a, Real-space images of all domain states. The circular coloured borders refer to the agglomerates indicated in c. b, Temporal evolution of the states. The background shades refer to the agglomerates. Dashed lines indicate times without data points. c, Transition network of the domain configurations. The distance between nodes approximately represents the Pearson distance of the corresponding states. The width of the connecting lines indicates the number of observed pair transitions. The diameter of the circular orange contours illustrates the total observed lifetime of each state. Background colours highlight state agglomerates. d, Magnification of the region marked with a magnifying glass in b. The displayed real-space images were reconstructed exclusively from the corresponding set of frames. e, Map of attractive (blue dots) and repulsive (red areas) pinning sites. The background shows the position of the domain walls and their relative occurrence in the internal modes. Scale bar, 500 nm.

Extended Data Fig. 1. Algorithm to calculate the magnetic pair correlations map.

a, The calculation starts with the experimental data, that is, the magnetic difference hologram h_diff(t) obtained at time t from the difference of a circular polarization hologram and a topography hologram. Inset, scanning electron micrograph of the sample, superimposed by an image of the magnetic domain state. Scale bar, 500 nm. b, Patterson map obtained from an inverse Fourier transformation of h_diff(t). The cross-correlation appears in the centre while the real-space magnetic-contrast image (‘reconstruction’) is offset from the centre by the object–reference distance. c, A low-pass filtered difference hologram is calculated from the Fourier transformation of the cross-correlation cropped from the Patterson map. Further normalization (flattening) is performed using the amplitudes of the topography scattering, i.e., the square-root of the reference-filtered topography hologram. d, Normalized pair correlation map calculated by the scalar product ⟨., .⟩ of the flattened difference holograms (equation (1). For illustration purposes, all panels are based on sequential averages of 100 hologram frames. See Methods for the mathematical steps.

Extended Data Fig. 2. Complete pair correlation map.

a, Pair correlation map of all recorded frames (indexed sequentially). b, Magnified section of the correlation map, marked with a red square in a, now plotted as a function of the wall time (time stamp) when the respective frames were recorded. Each block represents a stack of 100 acquired frames. White areas indicate time intervals where no images were recorded, mostly due to helicity change events.

Extended Data Fig. 3. Signal-to-noise ratio of the real- and Fourier-space method of calculating correlation maps.

a, Fourier-space correlation map calculated with the algorithm presented in Extended Data Fig. 1, showing a transition between two states. b, The same correlation map calculated using single-frame real-space reconstructions (see Extended Data Fig. 1b). c, Histograms showing the distribution of observed pair correlation values. The distributions were obtained from the same-state regions in each of the correlation maps (visible as yellow regions in a). To estimate the signal-to-noise ratio (SNR), both distributions were fitted with a Gaussian function. We define the SNR by the expectation value divided by the standard deviation of the fit. We find that the Fourier-space SNR is more than 10 times higher (29.3 ± 1.0) than the real space SNR (SNR 2.5 ± 0.2).

Extended Data Fig. 4. Discretization of the internal domain modes.

a, Creation of binary internal domain modes. The up and down magnetization of all domain images is binarized using image segmentation based on threshold filtering of the CDI reconstructions. The representations of images with a low signal-to-noise ratio were adjusted manually. b, Illustration of the multi-level discretization of internal domain modes. The CDI reconstruction of a domain image is decomposed into a set of binarized internal modes. The binary images of the internal modes are superimposed to create a discretized representation of the domain image with multiple contrast level. A fitting process determines the weighting coefficients from the image of the domain mode. For further details about the procedure, see Methods. Scale bar, 500 nm.

Extended Data Fig. 5. Sensitivity limit of the temporal reconstruction.

Frame misclassification probability of a two-state system as a function of the similarity of the underlying two domain states. A similarity value of one corresponds to indistinguishable states. Data points below 87% similarity show a misclassification probability of zero and were therefore excluded from the log-log plot. The light-blue band is a guide to the eye. Our sensitivity threshold is marked by the dashed blue lines. The horizontal line indicates the largest acceptable misclassification rate for temporal assignment (1%). The vertical line depicts the maximum similarity of two states before and after a temporally resolved transition (93.8%), which was chosen such that all data points left of this line are below the misclassification threshold. For further details, see Methods.

Extended Data Fig. 6. Overview of the reconstructed discretized internal modes.

We identified a total of 72 internal modes, ranging up to 99% in similarity (see Methods). The modes are subsets of the 32 domain states (see Fig. 4), as indicated by the grey background shading. Modes are defined by a high pair correlation of >93.8%, which means that their exact temporal sequence is inaccessible but statistical information, such as the real-space images and the number of contributing frames, can still be reconstructed reliably. Scale bar, 500 nm.

Extended Data Fig. 7. Statistical analysis of the real-space reconstructions.

a, Average of all domain configurations observed during the experiment weighted according to the number of frames for each configuration. b, Similar average of the discretized domain configurations. c, Superposition (sum) of the domain wall positions of all internal modes, normalized by the total number of modes. d, Average curvature of the domain walls. Only walls showing a considerable curvature are visualized in colour. Grey lines mark remaining domain walls. e, Number of magnetization switching events observed locally in the temporal evolution of the domain configuration. Scale bar, 500 nm.

Extended Data Fig. 8. Illustration of the conceptual difference between attractive and repulsive pinning.

String-shaped magnetic domain walls (grey lines) located in an energy landscape with attractive and repulsive Gaussian-shaped pinning potentials. The attractive pinning sites (blue) induce depressions in the energy landscape trapping the domain walls at their minimum, whereas the repulsive pinning site (red) forms an area-like potential barrier repelling the domain walls.

Extended Data Fig. 9. Domain-wall rearrangement during transition between two states.

a,b, Selected examples for inter-agglomerate (a) and intra-agglomerate (b) transitions. The colour code is explained below both panels. The summed contrast shows areas without magnetization changes as purple or white and areas with switched magnetization as blue or red. Areas containing repelling pinning sites are marked with semi-transparent grey shadows, whereas attractive pinning sites are marked with black dots. Scale bar, 500 nm.

Extended Data Fig. 10. Dendrogram of state agglomeration.

An UPGMA hierarchical clustering algorithm groups the 32 domain states shown in Fig. 4 into 11 agglomerates based on the state’s similarity distances and the frequency of transitions between the states. The separation threshold was manually set at a generally large step in the hierarchical distance (0.38) as indicated by the dashed red line. The colour coding separates the different agglomerates and corresponds to Fig. 4. Single, short-lived states which are not colour-coded in Fig. 4 are shown in grey here.