Magnetically mediated hole pairing in fermionic ladders of ultracold atoms

Abstract

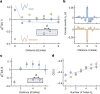
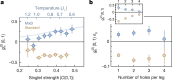
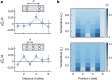
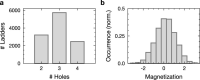
Conventional superconductivity emerges from pairing of charge carriers-electrons or holes-mediated by phonons¹. In many unconventional superconductors, the pairing mechanism is conjectured to be mediated by magnetic correlations², as captured by models of mobile charges in doped antiferromagnets³. However, a precise understanding of the underlying mechanism in real materials is still lacking and has been driving experimental and theoretical research for the past 40 years. Early theoretical studies predicted magnetic-mediated pairing of dopants in ladder systems^4-8, in which idealized theoretical toy models explained how pairing can emerge despite repulsive interactions⁹. Here we experimentally observe this long-standing theoretical prediction, reporting hole pairing due to magnetic correlations in a quantum gas of ultracold atoms. By engineering doped antiferromagnetic ladders with mixed-dimensional couplings¹⁰, we suppress Pauli blocking of holes at short length scales. This results in a marked increase in binding energy and decrease in pair size, enabling us to observe pairs of holes predominantly occupying the same rung of the ladder. We find a hole-hole binding energy of the order of the superexchange energy and, upon increased doping, we observe spatial structures in the pair distribution, indicating repulsion between bound hole pairs. By engineering a configuration in which binding is strongly enhanced, we delineate a strategy to increase the critical temperature for superconductivity.

Fig. 1. Hole pairing in mixD ladders.

a, Binding mechanism in the t−J ladders. Depicted are ladder systems with spin exchange J_⊥ ≫ J_∥ that form strong singlet bonds along the rungs. When a single hole from (i) moves through the system, as illustrated in (ii), it breaks the spin order by displacing the singlet bonds. (iii) The magnetic energy cost can be avoided if the second hole restores the spin order by moving together with the first hole. b, Pauli blocking of holes. Owing to their fermionic nature, holes repel each other along all directions according to the tunnelling amplitudes t_⊥ and t_∥. Close-distance hole pairs are thus energetically unfavourable. In mixD systems, a potential offset Δ between the two legs suppresses tunnelling t_⊥ and Pauli repulsion only occurs along the legs. Holes on the same rung can thus benefit from the binding mechanism, forming tightly bound pairs with a large binding energy. c, Average density of the mixD L = 7 ladder system with Δ ≈ U/2. d, Single experimental shot with two holes on the same rung, exemplifying the bunching of holes in the mixD system. a.u., arbitrary units. Source data

Fig. 2. Hole pairing in mixD versus standard ladders.

a, Hole–hole correlator $g_{\mathrm{h}}^{\left(2\right)}\left(d,1\right)$ between sites on opposite legs (as illustrated in the inset) for mixD (blue) and standard (brown) ladders with two to four holes per ladder. The strong correlation at d = 0 corresponds to two holes on the same rung. Correlations at this distance are strongly enhanced in the mixD system (pairing) and strongly suppressed in the standard ladders (repulsion). The blue line is calculated using MPS at finite temperature k_BT = 0.8 J_⊥ and corrected by the experimental detection fidelity (Methods). b, Excess events δ_h(d) of the same data, that is, the likelihood of finding holes at distance d compared with the infinite-temperature distribution. c, Hole–hole correlation on the same leg $g_{\mathrm{h}}^{\left(2\right)}\left(d,0\right)$ in the mixD system, showing that holes repel each other within the same leg. A finite-size offset correction has been applied to this subfigure (Methods). d, Spin–spin correlations C(0, 1) for spins on the same rung depending on the number of holes in the system. The lines represent linear fits. The larger slope indicates that the spin order of the standard system (brown) is more strongly disturbed by holes than the spin order of the mixD system (blue), where paired holes leave the spin order largely unperturbed. The error bars denote one s.e.m. and are smaller than the marker when not visible. Error bars in a, c and d are estimated using bootstrapping. Source data

Fig. 3. Temperature and doping dependence of hole pairing.

a, Rung hole–hole correlation $g_{\mathrm{h}}^{\left(2\right)}\left(0,1\right)$ for the mixD (blue) and standard (brown) ladders binned by the rung spin correlations C(0, 1) of the system. The temperature of the mixD system (top axis) is estimated by comparing the spin correlations (lower axis) with the theoretical values. The solid line is calculated using MPS and is corrected by the experimental detection fidelity. We see unbinding of pairs at low singlet strength, that is, high temperature. b, The hole correlator scaled with the hole density $g_{\mathrm{h}}^{\left(2\right)}(0,1)n_{\mathrm{h}}$ depending on the number of holes per leg for the mixD (blue) and standard (brown) ladders. Within our error bars, we find the hole binding to be independent of doping. The inset shows the correlator $g_{\mathrm{h}}^{\left(2\right)}\left(0,1\right)$, where the dashed line is a fit with the inherent 1/n_h scaling of the correlator. Error bars denote the bin width of the spin correlations (a) and the s.e.m. of the correlator (a and b). Source data

Fig. 4. Distribution of rung hole pairs in the mixD system.

a, Measured pair–pair correlation $g_{\mathrm{pair}}^{\left(2\right)}\left(d\right)$ of rung hole pairs in the experimental system. The upper plot shows the pair–pair correlation for four to five holes, that is, up to two pairs, in the system. The lower plot shows the pair–pair correlation for six to seven holes, that is, up to three pairs in the system. A finite-size offset correction has been applied to the curves (Methods). Error bars were estimated using bootstrapping. b, Theoretical (MPS) results for the density of rung pairs in the system for temperatures from 0.1 J_⊥ to 0.7 J_⊥. The upper plot shows the pair density for four holes. The lower plot shows the pair density for six holes. In both cases, the pairs maximize their respective distance, while also avoiding the edge of the system. Source data

Extended Data Fig. 1. Preparation sequence for mixD systems.

a, We first prepare nearly uncoupled 1D chains in which the leg tunnelling exceeds the rung coupling. b, While the legs are decoupled, we apply the offset Δ to one leg of the ladder. c, The final parameters are reached by ramping down the leg coupling and ramping up the rung coupling. There, the potential offset Δ between legs prevents tunnelling from one leg to the other. Note that in the final configuration J_⊥ ≫ J_∥.

Extended Data Fig. 2. Calibration of the optical potential offset.

The experimental sequence is run for different value of Δ in a regime close to unit occupancy of the lattice. tunnelling from one leg to the other is suppressed as long as ∣Δ − U∣ > 0. When Δ ~ U, tunnelling is possible, and an increased number of doublons in the system is measured.

Extended Data Fig. 3. Density of the mixD system without doublons.

The density of the mixD system, where only ladders without double occupancies are taken into account.

Extended Data Fig. 4. Hole and magnetization statistics.

a,b, Experimental distribution of holes per ladder (a) and total magnetization (b) for the data shown in Fig. 2a–c, and Fig. 3a.

Extended Data Fig. 5. Temperature estimation.

a, Singlet strength versus temperature. The calibration of temperature is performed using MPS data containing two to four holes. b, Experimental singlet strength and c, inferred temperature distributions. We evaluate our rung spin correlations C(0, 1) on the mixD system, using a time window of about 24 h. The temperature is extracted from C(0, 1) using the MPS simulation (a).