Twist response of actin filaments

Abstract

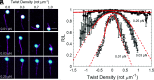
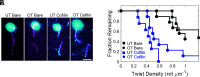
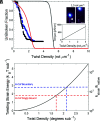
Actin cytoskeleton force generation, sensing, and adaptation are dictated by the bending and twisting mechanics of filaments. Here, we use magnetic tweezers and microfluidics to twist and pull individual actin filaments and evaluate their response to applied loads. Twisted filaments bend and dissipate torsional strain by adopting a supercoiled plectoneme. Pulling prevents plectoneme formation, which causes twisted filaments to sever. Analysis over a range of twisting and pulling forces and direct visualization of filament and single subunit twisting fluctuations yield an actin filament torsional persistence length of ~10 µm, similar to the bending persistence length. Filament severing by cofilin is driven by local twist strain at boundaries between bare and decorated segments and is accelerated by low pN pulling forces. This work explains how contractile forces generated by myosin motors accelerate filament severing by cofilin and establishes a role for filament twisting in the regulation of actin filament stability and assembly dynamics.

Keywords: actin; cofilin; plectoneme; severing; torsion.

Fig. 1.

Twisting actin filaments with magnetic tweezers. (A) Cartoon schematic of the experimental setup. Alexa 488–labeled actin filament seeds (green) were attached to a Biotin-PEG-Silane surface through biotin (yellow circles) and neutravidin (black diamonds) interactions and elongated from the barbed ends with Alexa 647–labeled actin (red). Filaments were further elongated from their barbed ends with digoxigenin (DIG)-labeled actin (purple). Paramagnetic beads (2.8 μm in diameter; gray) coated with DIG antibodies (purple) were attached to filaments at or near their barbed ends. Filament-attached beads can be rotated by a permanent magnet (blue and red rectangles) and pulled by buffer flow (black arrow). Relative filament and bead sizes are not drawn to scale. Twisting clockwise or counterclockwise corresponds to under- or overtwisting, respectively. (B) Rotation of a phalloidin-decorated filament attached to two paramagnetic beads. (C) Cosine of the rotational angle of the second paramagnetic bead (black trace) and the magnet (red trace) indicates that the bead and magnet rotation are in phase. (D) Rotation of an Alexa 647–labeled actin filament with visible attachment to paramagnetic bead indicates that the bead and filament rotation are in phase.

Fig. 2.

Actin filament force–extension response. (A) Representative fluorescent images of Alexa 647–labeled actin filaments (magenta) conjugated to a paramagnetic bead (cyan) under fluid flow. No magnetic field is applied. (B) Force–extension curves for actin filaments of varying lengths (colored points) with the global best fit to Eq. 1 (colored lines) with pulling forces at d = r (Methods). (C) Average force–extension curves, normalized to filament lengths, for 7 actin filaments and corresponding theory with the global best fit persistence length of 10.7 (±1) µm (solid red line) (Eq. 1). Theoretical force–extension curves (Eq. 1) in descending order with L_B = 100, 5, 1, and 0.1 µm (dashed red lines). Uncertainty bars indicate standard error of the mean (SEM).

Fig. 3.

Actin filament twist–extension response and supercoiling. (A) Representative fluorescent images of actin filament twist–extension with 0.01 (Top), 0.03 (Middle), and 0.25 (Bottom) pN pulling force (SI Appendix, Eq. S1 with d = r). (Scale bar, 5 µm.) (B) Twist–extension curves for actin filaments under 0.01 (white circles), 0.03 (gray circles), and 0.25 (black circles) pN pulling forces with the global best fit to Eq. 3 (red lines). Solid and dashed red lines differentiate model before and after plectoneme formation, respectively. Rotations along the positive x-axis indicate filament overtwisting, and rotations along the negative x-axis indicate undertwisting. The complete dataset represents 50 filaments and n > 3 for each experimental condition. Uncertainty bars represent SEM. The asymmetric look of red dashed fitting lines for over- and undertwists under the same pulling force is due to the different fixed parameters $\overline{\left(\frac{1}{L}\right)}$ in the fitting (Methods) and not because of differences in response to applied over- and undertwist.

Fig. 4.

Direct visualization of actin filament twisting fluctuations. (A) Cartoon schematic of the experimental setup. A cylindrical magnet with a center hole was positioned 5 mm above the coverslip surface–anchored actin filament (i.e., in the z direction perpendicular to the surface). A DIG-coated marker bead was added to the paramagnetic bead to track rotations. No flow was applied during experiments. Filament length and bending are not to scale. (B) (a) Assay is set up by identifying a filament attached to a paramagnetic bead (large dim bead) with identifiable marker beads (small bright bead) under fluid flow. (b) Fluid flow is turned off. (c) Cylindrical magnet is lowered into position. (d) Filament is pulled out of the focal plane. (e) Focal plane is adjusted to observe the rotational fluctuations of both beads. Images were taken every 5 s. (C) Example images of the angular fluctuations of the filament visualized by the absolute angle of a line connecting the two beads to the x direction. (D) The mean-subtracted absolute angle (SI Appendix, Eq. S25) of the marker beads over time. Black trace indicates the angular fluctuations from the filament tracked in (C). Gray traces represent four other sample traces from different experiments performed at different times. Histogram represents the distribution of absolute angles from the black trace. The actin filament torsional persistence length of 12.9 (±2.4) μm is an average (n = 5) of separate measurements, each was determined from the value of the variance at long times (see Panel E) and the filament length according to Eq. 4. (E) Time-dependent variance of the traces in D. It demonstrates that the measurement time of whole filament angular fluctuation has to be long enough for the variance to reach equilibrium such that experiencing all possibilities.

Fig. 5.

Torsional persistence length of actin filaments determined by electron cryomicroscopy. (A) Cartoon schematic of measured filament subunit twisting fluctuations. The top cartoon depicts an actin filament (gray) with the average, intrinsic twist (Δφ_1intrinsic) between adjacent subunits i and i+1 illustrated as a red curved arrow. The observed twist deviates from the intrinsic twist, either over or under, because of thermal fluctuations. The middle and bottom cartoons illustrate an undertwisted filament (light gray) overlaying a canonical filament with an intrinsic twist (dark gray). Blue arrows illustrate the observed twist between subunits i and i+1 (Middle) or i and i+3 (Bottom), which differs from the intrinsic twist by Δφ’_n (illustrated by black arrows). (B) Histograms of actin filament subunit twist fluctuations (Δφ’_n, in degrees) estimated from cryo-EM alignment parameters (reference volume of 5 subunits) for n = 1, 10, and 50 subunits. Red lines represent fits to a normal distribution with mean zero and variance $({\sigma }_{obs,n+1}^2$). (C) n dependence of the twist variance (${\sigma }_{obs,n+1}^2$). The solid red lines represent the best fit to SI Appendix, Eq. S21.

Fig. 6.

Twisted cofilactin filaments fragment more easily than twisted bare actin filaments. (A) Representative images of twist-induced fragmentation for undertwisted (UT) bare, overtwisted (OT) bare, undertwisted cofilin saturated, and overtwisted cofilin saturated filaments. (Scale bar, 4 µm.) (B) Survival analysis from the experiments in (A) at a pulling force of 0.03 pN. Log-rank test comparing UT bare to UT cofilin (P < 0.0001) and OT bare and OT cofilin (P = 0.0094). Both log-rank tests and Gehan–Breslow–Wilcoxon tests yielded similar P values, which conclude that the observed twisting response of bare and cofilin-decorated filaments is statistically different.

Fig. 7.

Modeling twist-induced fragmentation of actin filaments. (A) Experimental actin filament survival curves for undertwisted (blue) and overtwisted (black) bare actin filaments at 0.25 pN pulling force (2 µL min⁻¹ flow rate) and a twisting rate of ω = 0.3 rot s⁻¹. Data include instances where fragmentation occurs close to the bead or surface interfaces. For comparison, the plot includes simulations of filament survival curves as a function of twist density (SI Appendix, Eq. S31) at the same twist rate of 0.3 rot s⁻¹ with a length of L = 15 µm (red trace), as that typical in our twist–extension experiments in this study, and a twist rate of ω = 2.2 rot s⁻¹ with a length L = 0.1 µm (gray trace). Inset image is an example of twist-induced fragmentation. Inset graph is the model-predicted filament torque (SI Appendix, Eq. S9). (B) Model-predicted twisting strain energy per subunit (left y-axis, SI Appendix, Eq. S4) and the relative increase in fragmentation rate constant of strained relative to relaxed, native filaments (right y-axis, SI Appendix, Eq. S28). Dashed lines indicate the model-predicted twisting strain energy for the twist density imposed at boundaries of human cofilin clusters (blue) and by singly isolated bound human cofilin (red).