Non-Ewald methods for evaluating the electrostatic interactions of charge systems: similarity and difference

Abstract

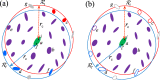
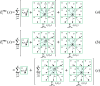
In molecular simulations, it is essential to properly calculate the electrostatic interactions of particles in the physical system of interest. Here we consider a method called the non-Ewald method, which does not rely on the standard Ewald method with periodic boundary conditions, but instead relies on the cutoff-based techniques. We focus on the physicochemical and mathematical conceptual aspects of the method in order to gain a deeper understanding of the simulation methodology. In particular, we take into account the reaction field (RF) method, the isotropic periodic sum (IPS) method, and the zero-multipole summation method (ZMM). These cutoff-based methods are based on different physical ideas and are completely distinguishable in their underlying concepts. The RF and IPS methods are "additive" methods that incorporate information outside the cutoff region, via dielectric medium and isotropic boundary condition, respectively. In contrast, the ZMM is a "subtraction" method that tries to remove the artificial effects, generated near the boundary, from the cutoff sphere. Nonetheless, we find physical and/or mathematical similarities between these methods. In particular, the modified RF method can be derived by the principle of neutralization utilized in the ZMM, and we also found a direct relationship between IPS and ZMM.

Keywords: Coulombic energy; Cutoff-based method; Electrostatic interaction; Electrostatic neutrality; Molecular dynamics; Non-Ewald method; Reaction field method.

Fig. 1

Schematic figures about “cavity” used in the RF method and interactions within the cavity are illustrated. Details are in Appendix B. (a) Conventional cavity: the set of atoms in ellipsoidal molecules within a red sphere (circle in 2D representation) is cavity for atom i and that within a blue sphere is cavity for $i^{\prime }$, where i and $i^{\prime }$ are atoms contained in a molecule a. A molecule including b, c, and e affect i, and molecules including b, d, e, and f affect $i^{\prime }$. Grey molecules partially affect either i or $i^{\prime }$, e.g., a molecule g partially affect i and does not affect $i^{\prime }$. A molecule f partially affects i and totally affects $i^{\prime }$. (b) New interpretation of cavity: cavity is the set of all atoms of solid ellipsoidal molecules, and it is common for atoms i and $i^{\prime }$. Open ellipsoidal molecules, including c, d, e, f, and g, do not affect both i and $i^{\prime }$. A molecule e, which is supposed to be totally charged, is excluded from the cavity; otherwise, it will violate the charge neutrality condition for the cavity (condition (b’) in the text). A molecule f, which is supposed to be charge neutral, is also excluded from the cavity; otherwise, the partial charge will violate the charge neutrality condition for the cavity

Fig. 2

Schematic figure of the three interpretations of the energy for atom i under the PBC, $E_i^{\text{PBC}}(x)$. The basic cell is the shaded region surrounded by image cells (only 8 cells are described using 2D representation). Small, closed circles represent atom i in the basic cell and its image atoms $i^{\prime }$, $i^{\prime \prime }$, $i^{\prime \prime \prime }$, ... in image cells. Small open circles represent atom j (≠i) in basic cell and its image atoms $j^{\prime }$, $j^{\prime \prime }$, $j^{\prime \prime \prime }$, ... in image cells. The “system” is composed from all atoms in the basic cell. (a) corresponds ordinary interpretation: $E_i^{\text{PBC}}(x)$ is the energy felt by iin the system from all atoms (all “j”s in the basic cell and all image “j”s in image cells, and all image “i”s). (b) and (c) correspond Eqs. 12b and 12c, respectively: $E_i^{\text{PBC}}(x)$ is the energy felt by the system from all “i”s (i in the basic cell and all image “i”s). Equation 12b represents the energy felt by “j”s in the system plus the energy felt by i in the system, while Eq. 12c represents the energy influenced from i in the system and the energy influenced from “i”s outside the system

Fig. 3

Schematic figure for representing the interactions used in the IPS method under the isotropic boundary condition. The center circle is the “local region” of atom i, a sphere with radius r_c, containing other atoms j, etc. $D_1^{(i)}$ [$D_2^{(i)}$] is a spherical shell (which is the annulus in this 2D representation) with a small radius r_c [3r_c] and a large radius 3r_c [5r_c]. $S_1^{(i)}$ [$S_2^{(i)}$] is a circle with a radius 2r_c [4r_c] and contained in $D_1^{(i)}$ [$D_2^{(i)}$]. Shown is only for m = 1,2. Dotted circles represent copies of the local region (called “image regions”), while, for calculating the interactions, the continuum approximation $S_1^{(i)},S_2^{(i)},\cdots$ are actually used instead, which can be viewed as continued images of $i^{\prime },i^{\prime \prime },\cdots ,$ respectively (see Appendix C (ii)). The “spherical interaction” (or “random interaction”) is interactions to atom j from spheres $S_1^{(i)},S_2^{(i)},\cdots$ (see Eq. 93). The “axial interaction” (Appendix C (iii)) is interactions to atom j from atoms $i^{\prime },i^{\circ },i^{\prime \prime },i^{\circ \circ },\cdots ,$ which are i’s copy along the j − i axis, ε_ij(R₁ − r_ij) + ε_ij(R₁ + r_ij) + ⋯ (see Eq. 94)

Fig. 4

Schematic figure for representing a neutralized subset ${\mathcal{M}}_i^{(l)}$ (composed from atoms in the green shaded region) in the cutoff sphere ${\mathcal{R}}_i$ with a radius r_c around atom i having charge + 1 denoted by “ + ” (while “−” denotes an atom with charge − 1). Excess subset ${\mathcal{J}}_i^{(l)}$ contains 5 positive charges, where, in particular, the 3 bold font “+ ” charges in the left side seem to provide a high energy state in the cutoff sphere

Fig. 5

Relationships among non-Ewald methods: Pre-averaging (PA) (Yakub and Ronchi 2003); FSw-Wolf (Fukuda et al. 2008); Wolf (Wolf et al. 1999); Harrison (Harrison 2006); modified reaction field (MRF) (Barker and Watts ; Fukuda and Nakamura 2012); generalized reaction field (GRF) (Hummer et al. 1994); modified IPSp (MIPSp) (Wu and Brooks ; and see Eq. 59); IPSn (Wu and Brooks 2005); zero multipole summation method (ZMM) (Fukuda 2013); non-damped ZMM (Nd-ZMM); and non-damped zero-dipole (Nd-ZD) (Fukuda et al. 2011). A dashed line shows an approximate relationship

Fig. 6

Scaled functions v − v(1) (Eq. (60)), which completely characterize the pair potential functions and become irrelevant to the cutoff length, are shown for the IPS method, the MRF method with 𝜖_RF = 5 (very similar to IPS), that with ${𝜖}_{\text{RF}}\to \infty$, the GRF method, ZMM with α = 0 and l = 4, ZMM with α = 0 and l = 3, and the general shifting method (GSM) with l = 1, 2, and 3. Panel (a) indicates for almost full scale 0.1 ≤ s ≤ 1 and (b) for 0.8 ≤ s ≤ 1