Estimating Temporally Variable Selection Intensity from Ancient DNA Data

Abstract

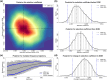
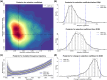
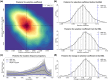
Novel technologies for recovering DNA information from archaeological and historical specimens have made available an ever-increasing amount of temporally spaced genetic samples from natural populations. These genetic time series permit the direct assessment of patterns of temporal changes in allele frequencies and hold the promise of improving power for the inference of selection. Increased time resolution can further facilitate testing hypotheses regarding the drivers of past selection events such as the incidence of plant and animal domestication. However, studying past selection processes through ancient DNA (aDNA) still involves considerable obstacles such as postmortem damage, high fragmentation, low coverage, and small samples. To circumvent these challenges, we introduce a novel Bayesian framework for the inference of temporally variable selection based on genotype likelihoods instead of allele frequencies, thereby enabling us to model sample uncertainties resulting from the damage and fragmentation of aDNA molecules. Also, our approach permits the reconstruction of the underlying allele frequency trajectories of the population through time, which allows for a better understanding of the drivers of selection. We evaluate its performance through extensive simulations and demonstrate its utility with an application to the ancient horse samples genotyped at the loci for coat coloration. Our results reveal that incorporating sample uncertainties can further improve the inference of selection.

Keywords: ancient DNA; demographic history; natural selection; particle marginal Metropolis-Hastings; sampling uncertainty; two-layer hidden Markov model.

Fig. 1.

Graphical representation of our two-layer HMM framework for the data on aDNA sequences, where $X$ denotes the population mutant allele frequency, $\mathit{G}$ denotes the sample individual genotypes, and $\mathit{R}$ denotes the sample individual reads.

Fig. 2.

Posteriors for the selection coefficients and the underlying frequency trajectory of the mutant allele in the population produced through our method from a data set of genotype likelihoods generated with the selection coefficients $s^{-}=0.0198$ and $s^{+}=-0.0081$. (a) Joint posterior for the selection coefficients $s^{-}$ and $s^{+}$. (b) Marginal posteriors for the selection coefficients $s^{-}$ and $s^{+}$. (c) Posterior for the underlying trajectory of the mutant allele frequency. (d) Posterior for the selection change $\mathrm{\Delta }s$.

Fig. 3.

Empirical distributions for the bias in MAP estimates of the selection coefficients across different data qualities and selection scenarios. Data qualities (scenarios A–F) are described in table 1, and selection scenarios (scenarios 1–9) are described in table 2. ($a$)–($i$) Boxplots of the bias for scenarios 1–9.

Fig. 4.

Empirical distributions for the bias in MAP estimates of the selection coefficient across different ranges of the selection coefficient $s$ with the parameters $\varphi =0.85$ and $\psi =1$ (i.e., scenario D in table 1).

Fig. 5.

ROC curves for testing a change in selection across different data qualities and selection scenarios. The AUC value for each curve is summarized. Data qualities (scenarios A–F) are described in table 1, and selection scenarios (scenarios 1–9) are described in table 2. ROC curves for (a) a negative change in selection and (b) a positive change in selection.

Fig. 6.

ROC curves for testing a change in selection across different ranges of the selection change $\mathrm{\Delta }s$ with the parameters $\varphi =0.85$ and $\psi =1$ (i.e., scenario D in table 1). The AUC value for each curve is summarized. ROC curves for (a) a negative change in selection and (b) a positive change in selection.

Fig. 7.

Posteriors for the selection coefficients of the ASIP mutation before and from horse domestication (starting from 3,500 BC) and the underlying frequency trajectory of the ASIP mutation in the population. The samples drawn before 12,500 BC are excluded. DOM stands for domestication. (a) Joint posterior for the selection coefficients $s^{-}$ and $s^{+}$. (b) Marginal posteriors for the selection coefficients $s^{-}$ and $s^{+}$. (c) Posterior for the underlying frequency trajectory of the ASIP mutation. (d) Posterior for the selection change $\mathrm{\Delta }s$.

Fig. 8.

Posteriors for the selection coefficients of the MC1R mutation before and from horse domestication (starting from 3,500 BC) and the underlying frequency trajectory of the MC1R mutation in the population. The samples drawn before 4,300 BC are excluded. DOM stands for domestication. (a) Joint posterior for the selection coefficients $s^{-}$ and $s^{+}$. (b) Marginal posteriors for the selection coefficients $s^{-}$ and $s^{+}$. (c) Posterior for the underlying frequency trajectory of the MC1R mutation. (d) Posterior for the selection change $\mathrm{\Delta }s$.

Fig. 9.

Posteriors for the selection coefficients of the KIT13 mutation before and from the Middle Ages (starting from AD 400) and the underlying frequency trajectory of the KIT13 mutation in the population. The samples drawn before 3645 BC are excluded. EMA stands for Early Middle Ages. (a) Joint posterior for the selection coefficients $s^{-}$ and $s^{+}$. (b) Marginal posteriors for the selection coefficients $s^{-}$ and $s^{+}$. (c) Posterior for the underlying frequency trajectory of the KIT13 mutation. (d) Posterior for the selection change $\mathrm{\Delta }s$.

Fig. 10.

Posteriors for the selection coefficients of the TRPM1 mutation before and from horse domestication (starting from 3,500 BC) and the underlying frequency trajectory of the TRPM1 mutation in the population. The samples drawn before 14,500 BC are excluded. DOM stands for domestication. (a) Joint posterior for the selection coefficients $s^{-}$ and $s^{+}$. (b) Marginal posteriors for the selection coefficients $s^{-}$ and $s^{+}$. (c) Posterior for the underlying frequency trajectory of the TRPM1 mutation. (d) Posterior for the selection change $\mathrm{\Delta }s$.