Vanishing Opinions in Latané Model of Opinion Formation

Abstract

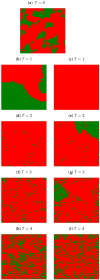
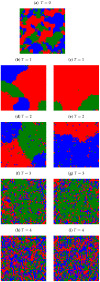
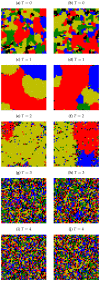
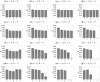
In this paper, the results of computer simulations based on the Nowak-Szamrej-Latané model with multiple (from two to five) opinions available in the system are presented. We introduce the noise discrimination level (which says how small the clusters of agents could be considered negligible) as a quite useful quantity that allows qualitative characterization of the system. We show that depending on the introduced noise discrimination level, the range of actors' interactions (controlled indirectly by an exponent in the distance scaling function, the larger the exponent, the more influential the nearest neighbors are) and the information noise level (modeled as social temperature, which increases results in the increase in randomness in taking the opinion by the agents), the ultimate number of the opinions (measured as the number of clusters of actors sharing the same opinion in clusters greater than the noise discrimination level) may be smaller than the number of opinions available in the system. These are observed in small and large information noise limits but result in either unanimity, or polarization, or randomization of opinions.

Keywords: clusterization and polarization; information noise; opinion dynamics; social impact; sociophysics.

Figure A1

Examples of two most probable spatial distributions of the final opinion after ${10}^3$ time steps. $L=41$, $\alpha =3$, $K=2$ and various levels of noise T.

Figure A2

Examples of two most probable spatial distributions of the final opinion after ${10}^3$ time steps. $L=41$, $\alpha =3$, $K=3$ and various levels of noise T.

Figure A3

Examples of two most probable spatial distributions of the final opinion after ${10}^3$ time steps. $L=41$, $\alpha =3$, $K=5$ and various levels of noise T.

Figure A4

Examples of two most probable spatial distributions of the final opinion after ${10}^3$ time steps. $L=41$, $\alpha =4$, $K=2$ and various levels of noise T.

Figure A5

Examples of two most probable spatial distributions of the final opinion after ${10}^3$ time steps. $L=41$, $\alpha =4$, $K=3$ and various levels of noise T.

Figure A6

Examples of two most probable spatial distributions of the final opinion after ${10}^3$ time steps. $L=41$, $\alpha =4$, $K=4$ and various levels of noise T.

Figure A7

Examples of two most probable spatial distributions of the final opinion after ${10}^3$ time steps. $L=41$, $\alpha =4$, $K=5$ and various levels of noise T.

Figure A8

Average number $\langle 𝐶\rangle$ of opinion clusters after $t={10}^3$ time steps for various exponents of the distance scaling function $\alpha$ and various numbers of available opinions K in the system. Noise discrimination threshold $\theta =12$. The system contains $L^2={41}^2$ actors. The results are averaged over $R=100$ independent system realizations.

Figure A9

Average number $\langle 𝐶\rangle$ of opinion clusters after $t={10}^3$ time steps for various exponents of the distance scaling function $\alpha$ and various numbers of available opinions K in the system. The noise discrimination threshold $\theta =25$. The system contains $L^2={41}^2$ actors. The results are averaged over $R=100$ independent system realizations.

Figure A9

Average number $\langle 𝐶\rangle$ of opinion clusters after $t={10}^3$ time steps for various exponents of the distance scaling function $\alpha$ and various numbers of available opinions K in the system. The noise discrimination threshold $\theta =25$. The system contains $L^2={41}^2$ actors. The results are averaged over $R=100$ independent system realizations.

Figure A10

Average number $\langle 𝐶\rangle$ of opinion clusters after $t={10}^3$ time steps for various exponents of the distance scaling function $\alpha$ and various numbers of available opinions K in the system. The noise discrimination threshold $\theta =50$. The system contains $L^2={41}^2$ actors. The results are averaged over $R=100$ independent system realizations.

Figure A11

The histograms of frequencies f of the number $\mathsf{\Phi }$ of surviving opinions after $={10}^3$ time steps and for various values of the distance scaling function exponent $\alpha$ and various values of the number of available opinions K. The system contains $L^2={41}^2$ actors. The noise discrimination level $\theta =12$ and the results are averaged over $R=100$ independent simulations.

Figure A12

The histograms of frequencies f of the number $\mathsf{\Phi }$ of surviving opinions after $={10}^3$ time steps and for various values of the distance scaling function exponent $\alpha$ and various values of the number of available opinions K. The system contains $L^2={41}^2$ actors. The noise discrimination level $\theta =25$ and the results are averaged over $R=100$ independent simulations.

Figure A13

The histograms of frequencies f of the number $\mathsf{\Phi }$ of surviving opinions after $={10}^3$ time steps and for various values of the distance scaling function exponent $\alpha$ and various values of the number of available opinions K. The system contains $L^2={41}^2$ actors. The noise discrimination level $\theta =50$ and the results are averaged over $R=100$ independent simulations.

Figure 1

Example of random initial state of the system for (a) $K=2$ and (b) $K=4$. Various colors correspond to various opinions.

Figure 2

The sketches of shapes of the neighborhoods closest to the sites (a) $n=1$, (b) $n=9$, (c) $n=25$, (d) $n=49$ sites. The values of the r parameters indicated in the figures in the headline influence summation limits in the nominator of Equation (7).

Figure 3

Examples of two most probable spatial distributions of the final opinion after ${10}^3$ time steps. $L=41$, $\alpha =3$, $K=4$ and various levels of noise T.

Figure 4

Average number $\langle 𝐶\rangle$ of opinion clusters after $t={10}^3$ time steps for the exponent of the distance scaling function $\alpha =3$, the number $K=4$ of opinions available in the system, and the noise discrimination threshold $\theta =25$. The system contains $L^2={41}^2$ actors. The results are averaged over $R=100$ independent system realizations.

Figure 5

The average ratio (in percents) of the size of the largest cluster $\langle {𝑆}_{\max }\rangle$ to the size of the entire system $L^2$ depending on the parameters $\alpha$ and T. $L=41$, $t={10}^3$, $R=100$.

Figure 6

The histogram of frequencies f of the number $\mathsf{\Phi }$ of surviving opinions for $\alpha =3$, $K=4$ and the level of noise discrimination $\theta =25$.

Figure 7

The most probable final number ${\mathsf{\Phi }}^{\star }$ of surviving opinions for various numbers K of opinions available in the system and noise discrimination thresholds $\theta$ depending on the level of information noise T and the range of interaction $\alpha$.

Figure 7

The most probable final number ${\mathsf{\Phi }}^{\star }$ of surviving opinions for various numbers K of opinions available in the system and noise discrimination thresholds $\theta$ depending on the level of information noise T and the range of interaction $\alpha$.