Precision Machine Learning

Abstract

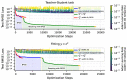
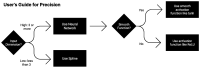
We explore unique considerations involved in fitting machine learning (ML) models to data with very high precision, as is often required for science applications. We empirically compare various function approximation methods and study how they scale with increasing parameters and data. We find that neural networks (NNs) can often outperform classical approximation methods on high-dimensional examples, by (we hypothesize) auto-discovering and exploiting modular structures therein. However, neural networks trained with common optimizers are less powerful for low-dimensional cases, which motivates us to study the unique properties of neural network loss landscapes and the corresponding optimization challenges that arise in the high precision regime. To address the optimization issue in low dimensions, we develop training tricks which enable us to train neural networks to extremely low loss, close to the limits allowed by numerical precision.

Keywords: ML for science; machine learning; optimization; scaling laws.

Figure A1

Rescaling loss has minimal benefit relative to boosting.

Figure A2

Low-curvature subspace training curves for varying thresholds $\tau$.

Figure A3

Scaling of tanh networks with the BFGS vs Adam optimizer. We use the same setup as in Figure 5, training tanh MLPs of depth 2–4 of varying width on functions given by symbolic equations. BFGS outperforms Adam on the 3-dimensional example shown (top left) and performs roughly similarly to Adam on the other problems.

Figure A4

Eigenvalues (dark green) of the loss landscape Hessian (MSE loss) after training a width-20, depth-3 network to fit $y=x^2$ with the BFGS optimizer. Like in Figure 7, we also plot the magnitude of the gradient’s projection onto each corresponding eigenvector (thin red line). The “canyon” shape of the loss landscape is more obvious at lower-loss points in the landscape found by BFGS than Adam finds. There is a clear set of top eigenvalues corresponding to a few directions of much higher curvature than the bulk.

Figure 1

In (a) (top), we show the solutions learned by a ReLU network and linear simplex interpolation on the 1D problem $y=cos\left(2x\right)$. In (b) (bottom), we visualize linear regions for a ReLU network, trained on unnormalized data (left) and normalized data (center), as well as linear simplex interpolation (right) on the 2D problem $z=xy$. In general, we find that normalizing data to have zero mean and unit variance improves network performance, but that linear simplex interpolation outperforms neural networks on low-dimensional problems by better vertex placement.

Figure 2

Scaling of linear simplex interpolation versus ReLU NNs. While simplex interpolation scales very predictably as $N^{-2/d}$, where d is the input dimension, we find that NNs sometimes scale better (at least in early regimes) as $N^{-2/d^{*}}$, where $d^{*}=2$, on high dimensional problems.

Figure 3

ReLU neural networks are seen to initially scale roughly as if they were modular. Networks with enforced modularity (dark blue and red, dashed line), with architecture depicted on the right, perform and scale similarly, though slightly better, than standard dense MLPs of the same depth (light blue and red).

Figure 4

Interpolation methods, both linear and nonlinear, on 2D and 3D problems, seen to approximately scale as $D^{-(n+1)/d}$ where n is the order of the polynomial spline, d is the input dimension.

Figure 5

Scaling of linear simplex interpolation vs tanh NNs. We also plot ReLU NN performance as a dotted line for comparison. While simplex interpolation scales very predictably as $N^{-2/d}$, where d is the input dimension, tanh NN scaling is much messier. See Appendix C for a comparison of scaling curves with Adam vs. the BFGS optimizer.

Figure 6

(a) Scaling of neural networks on a target function which can be arbitrarily closely approximated by a network of finite width. (b) diagram from [35] showing how a four-neuron network can implement multiplication arbitrarily well. Therefore a depth-2 network of width at least 12 has an architecture error at the machine precision limit, yet optimization in practice does not discover solutions within at least 10 orders of magnitude of the precision limit.

Figure 7

Eigenvalues (dark green) of the loss landscape Hessian (MSE loss) after training with the Adam optimizer, along with the magnitude of the gradient’s projection onto each corresponding eigenvector (thin red line). We see a cluster of top eigenvalues and a bulk of near-zero eigenvalues. The gradient (thin jagged red curve) points mostly in directions of high-curvature. See Appendix D for a similar plot after training with BFGS rather than Adam.

Figure 8

Comparison of Adam with BFGS + low-curvature subspace training + boosting. Using second-order methods like BFGS, but especially using boosting, leads to an improvement of many orders of magnitude over just training with Adam. Target functions are a teacher network (top) and a symbolic equation (bottom).

Figure 9

Comparison of Adam with BFGS + low-curvature subspace training + boosting, for a 2D problem (top) and a 6D problem (bottom), the equation we studied in Figure 6a. As we increase dimension, the optimization tricks we tried in this work show diminishing benefits.

Figure 10

User’s Guide for Precision: which approximation is best depends on properties of the problem.