Brillouin Scattering Study of Electro-Optic KTa1- xNb x O3 Crystals

Abstract

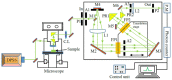
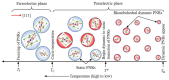
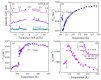
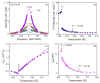
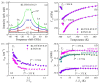
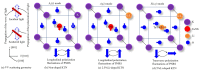
The functionality enhancement of ferroelectrics by local polar clusters called polar nanoregions (PNRs) is one of the current interests in materials science. KTa_1-xNb_xO₃ (KTN) with perovskite structure is a well-known electro-optic crystal with a large Kerr effect. The existence of PNRs in relaxor-like ferroelectric Nb-rich KTN with homovalent B-site cations is controversial. This paper reviews recent progress in understanding precursor dynamics in Nb-rich KTN crystals studied using Brillouin scattering. The intense central peak (CP) and significant softening of sound velocity are observed above the Curie temperature (T_C) due to the polarization fluctuations in PNRs. The effects of Li-doping, defects, and electric fields on the growth and/or creation of PNRs are found using changes in acoustic properties. The electric-field-induced T_C, which is shifted to higher values with increases in applied voltage, including critical endpoint (CEP) and field gradient by trapped electrons, are discussed as well. This new knowledge may give new insight into advanced functionality in perovskite ferroelectrics.

Keywords: Brillouin scattering; ferroelectric; macro- and nanodomains; perovskite; polar nanoregions; random fields.

Figure 1

A schematic illustration of a Sandercock 3 + 3 pass tandem interferometer equipped with a photomultiplier and optical microscope [57,58].

Figure 2

A schematic illustration of the temperature evolution of PNRs in relaxor-like KTN crystals based on the inelastic light scattering results. Red denotes the dynamic PNRs and blue indicates static PNRs, where the arrow denotes the orientation of PNRs. The dynamic PNRs appear at the so-called Burns temperature, T_B. Upon cooling, the size of the dynamic PNRs increases slowly and dynamic PNRs become more sluggish due to the cooperative interaction with the neighboring PNRs. Eventually, the dynamic PNRs start to become static PNRs at the intermediate temperature, T*. For further cooling, the size of PNRs becomes intense due to their growth in addition to the merger of neighboring PNRs.

Figure 3

(a) The observed Brillouin spectra of non-doped KTN/0.40 single crystal at some selected temperatures measured with FSR = 75 GHz. (b) The longitudinal velocity of the LA mode, and (c) the transverse velocity of the TA mode in a KTN/0.40 single crystal as a function of temperature. (d) The temperature dependence of the longitudinal sound attenuation in a KTN/0.40 single crystal. The short dashed and solid lines in (c) and (d) are the guide to eyes and the best fit result obtained using Equation (7), respectively. The inset in figure (d) exhibits the plot on a large scale to denote the T*. The data were adapted from Refs. [25,58].

Figure 4

(a) Brillouin scattering spectra the KTN/0.40 crystal at selected temperatures measured with FSR = 300 GHz, where the solid lines denote the curves fitted using the Voigt function. (b) The CP intensity of the KTN/0.40 crystal as a function of temperature. (c) The temperature dependence of the inverse of the relaxation time determined from the CP width, where the solid line is the result of best fit using Equation (9). (d) The mean size of the dynamic PNRs of KTN/0.40 single crystal as a function of temperature. The data were adapted from Refs. [25,58].

Figure 5

(a) Brillouin scattering spectra of the KLTN/0.05/0.27 single crystal at some selected temperatures recorded with FSR = 75 GHz. (b) Temperature-dependent elastic constant C₁₁ of both KTN/0.40 and KLTN/0.05/0.27 single crystals. The solid lines are the best fit result obtained from Equation (11) (c) The attenuation of the TA mode in the KTN/0.40 and KLTN/0.05/0.27 crystals as a function of T/T_C. (d) The observed frequency shift of the TA mode of KTN/0.40, KLTN/0.025/0.38, and KLTN/0.05/0.27 crystals as a function of normalized temperature. The short dashed lines are guides to the eyes. The data were adapted from Refs. [27,58].

Figure 6

(a) The CP spectra of KTN/0.40 and the KLTN/0.05/0.27 single crystals measured with the FSR = 300 GHz at 353 K. (b) The CP intensity of KTN/0.40 (solid diamonds) and KLTN/0.05/0.27 (solid triangles) single crystals as a function of T/T_C. (c) The inverse of the relaxation time estimated from the width of the CP of non-doped KTN, 2.5%Li-doped KTN, and 5%Li-doped KTN single crystals as a function of normalized temperature. The solid lines are the lines fit with Equation (12) (d) The size of a dynamic PNR of non-doped KTN and 5%Li-doped KTN crystals as a function of T/T_C. The data were adapted from Refs. [27,58].

Figure 7

(a) A typical depiction of the VV scattering geometry. A schematic interpretation of the polarization fluctuations of PNRs caused by A₁(z) mode in (b) non-doped KTN, (c) 2.5%Li-doped KTN, and E(x,y) mode in (d) 5%Li-doped KTN crystals observed in the VV scattering under the condition of fixed A-site cations [103].

Figure 8

A schematic illustration of the lattice showing the location of substituents in the cubic perovskite, (a) non-doped KTN, (b) 2.5%Li-doped KTN, and (c) 5%Li-doped KTN single crystals, where a small percentage of Li ions occupy the B-site in 5%Li-doped KTN and the Li ions only occupy the A-site in 2.5%Li-doped KTN. The total energy per formula unit obtained using the density functional theory (DFT) calculation as a function of the Li content (d) at the A-site (e) near the 5%Li-doping at the A-site and (f) at A- and B-sites of the Li-doped KTN/0.27 single crystal. The data were adapted from Ref. [103].

Figure 9

Schematic illustration of (a) spatial heterogeneity and (b) spatial dependence of T_C in a composition gradient on Li-doped KTN wafer. Diamonds (blue) and closed circles (red) denote the regions with high and low defect density, respectively. The elastic constants (c) C₁₁ and (d) C₄₄ of a composition gradient Li-doped KTN wafer as a function of position. The data were adapted from Refs. [58,111].

Figure 10

(a) Brillouin scattering spectra of the KLTN/0.05/0.26 single crystal at some selected temperatures measured at zero field cooling (ZFC). (b) The temperature dependence of the frequency shift of the TA mode of the KLTN/0.05/0.26 single crystal. (c) The Brillouin scattering spectra of the KLTN/0.05/0.26 crystal at some selected electric fields measured in the ferroelectric phase under a constant temperature of 291 K, where the electric field was applied along the [100] direction. (d) The frequency shift of the TA mode observed in the ferroelectric phase as a function of electric fields. (e) The typical Brillouin spectra of the KLTN/0.05/0.26 crystal at some selected temperatures measured under ZFC and field cooling (FC) at 1.20 kV/cm. (f) The temperature dependence of the FWHM of the LA mode observed under ZFC and FC process [113].

Figure 11

(a) The CP intensity of the KLTN/0.05/0.26 crystal at some selected temperatures as a function of applied voltage. (b) Temperature dependence of critical electric voltages of a phase transition, where V_C2 denotes the transition from ferroelectric to paraelectric and V_C1 indicates the transition from paraelectric to ferroelectric phase. (c) The dielectric constants of the KLTN/0.05/0.26 crystals measured at 1 kHz under the DC biasing voltages as a function of temperature. The electric voltage dependence of the observed CP intensity at (d) close to the anode (position 1), (e) close to the center (position 2), and (f) close to the cathode (position 3). The three positions in the KLTN/0.05/0.26 crystal are schematically drawn in (g). (h) The critical electric field of the KLTN/0.05/0.26 crystal as a function of position. The data were adapted from Ref. [116].