Self-Oscillating Curling of a Liquid Crystal Elastomer Beam under Steady Light

Abstract

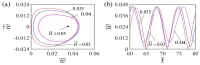
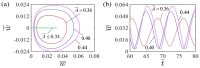
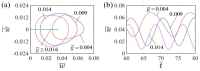
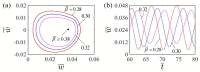
Self-oscillation absorbs energy from a steady environment to maintain its own continuous motion, eliminating the need to carry a power supply and controller, which will make the system more lightweight and promising for applications in energy harvesting, soft robotics, and microdevices. In this paper, we present a self-oscillating curling liquid crystal elastomer (LCE) beam-mass system, which is placed on a table and can self-oscillate under steady light. Unlike other self-sustaining systems, the contact surface of the LCE beam with the tabletop exhibits a continuous change in size during self-sustaining curling, resulting in a dynamic boundary problem. Based on the dynamic LCE model, we establish a nonlinear dynamic model of the self-oscillating curling LCE beam considering the dynamic boundary conditions, and numerically calculate its dynamic behavior using the Runge-Kutta method. The existence of two motion patterns in the LCE beam-mass system under steady light are proven by numerical calculation, namely self-curling pattern and stationary pattern. When the energy input to the system exceeds the energy dissipated by air damping, the LCE beam undergoes self-oscillating curling. Furthermore, we investigate the effects of different dimensionless parameters on the critical conditions, the amplitude and the period of the self-curling of LCE beam. Results demonstrate that the light source height, curvature coefficient, light intensity, elastic modulus, damping factor, and gravitational acceleration can modulate the self-curling amplitude and period. The self-curling LCE beam system proposed in this study can be applied to autonomous robots, energy harvesters, and micro-instruments.

Keywords: curling; dynamic boundary problem; liquid crystal elastomer; optically-responsive; self-oscillation.

Figure 1

(a) Schematic diagram of the dynamic model of the LCE beam-mass system for self-sustained curling under steady light. (b) Equivalent schematic of the right half of the system in Figure 1a, where the LCE beam is partially in contact with the table. (c) Magnified cross-sectional view of the LCE beam, showing the optically-driven strain distribution on the beam section, with the lower surface of the LCE beam covered with a light-shielding layer. (d) Force analysis of the mass block at the end of the LCE beam, which is subjected to the mass gravity mg, the air damping force $F_{\mathrm{f}}$, and the elastic force $F_{\mathrm{L}}$ provided by the LCE beam. (e) Force analysis of the untouched part of the LCE beam, which is subjected to the elastic force $F_{\mathrm{L}}$, the crosssection shear force $F_{\mathrm{s}}$, and crosssection bending moment $M\left(x_{\mathrm{c}}\right)$ provided by the touched part of LCE beam. Under steady light, the LCE beam can self-curl periodically.

Figure 2

(a) Time history and (b) phase trajectory diagram of the stationary pattern of the LCE beam-mass system for $\overline{H}=0.04$, $\overline{A}=0.36$, ${\overline{I}}_0=0.058$, $\overline{E}=2.4$, $\overline{g}=0.015$, $\overline{\beta }=0.30$ and $\overline{\dot{w}}=0$. (c) Time history and (d) phase trajectory diagram of the self-curling pattern of the LCE beam-mass system for $\overline{H}=0.04$, $\overline{A}=0.36$, ${\overline{I}}_0=0.06$, $\overline{E}=2.4$, $\overline{g}=0.015$, $\overline{\beta }=0.30$ and $\overline{\dot{w}}=0$. Two motion patterns exist for the LCE beam-mass system under steady light: the stationary pattern and the self-curling pattern.

Figure 3

(a) Time dependence of the cis-number fraction of the LCE beam; (b) Time dependence of the curvature of the LCE beam; (c) Time dependence of the elastic force of the LCE beam; (d) Dependence of the elastic force on the displacement of the mass block. (e) Time dependence of the damping force; (f) Dependence of the damping force on the displacement of the mass block. The area enclosed in Figure 3d indicates the net work done by the elastic force, which is equal to the energy dissipated by the damping, i.e., the self-curling pattern is maintained.

Figure 4

Effect of dimensionless light source height on the self-curling of the LCE beam-mass system for the other parameters $\overline{A}=0.36$, $\overline{E}=2.4$, ${\overline{I}}_0=0.06$, $\overline{g}=0.015$, $\overline{\beta }=0.30$ and $\overline{\dot{w}}=0$. (a) Limit cycles; (b) Time histories for different light source heights $\overline{H}$. Both amplitude and period of the self-curling increase as the light source height $\overline{H}$ increases.

Figure 5

Effect of dimensionless curvature coefficient on the self-curling of the LCE beam-mass system for the other parameters $\overline{H}=0.04$, $\overline{E}=2.4$, ${\overline{I}}_0=0.06$, $\overline{g}=0.015$, $\overline{\beta }=0.30$ and $\overline{\dot{w}}=0$. (a) Limit cycles; (b) Time histories for different curvature coefficients $\overline{A}$. As the dimensionless curvature coefficient increases, the self-curling amplitude increases significantly, while the self-curling period remains almost constant.

Figure 6

Effect of dimensionless light intensity on the self-curling of the LCE beam-mass system for the other parameters $\overline{H}=0.04$, $\overline{A}=0.36$, $\overline{E}=2.4$, $\overline{g}=0.015$, $\overline{\beta }=0.30$ and $\overline{\dot{w}}=0$. (a) Limit cycles; (b) Time histories for different light intensities ${\overline{I}}_0$. As the light intensity ${\overline{I}}_0$ increases, the self-curling amplitude displays a significant increase, while the self-curling period remains almost unchanged. Figure 6 presents the effect of different light intensities ${\overline{I}}_0$ on the self-curling of the LCE beam. In the calculation, we set the other parameters $\overline{H}=0.04$, $\overline{A}=0.36$, $\overline{E}=2.4$, $\overline{g}=0.015$, $\overline{\beta }=0.30$ and $\overline{\dot{w}}=0$.

Figure 7

Effect of dimensionless elastic modulus on the self-curling of the LCE beam-mass system for the other parameters $\overline{H}=0.04$, $\overline{A}=0.36$, ${\overline{I}}_0=0.06$, $\overline{g}=0.015$, $\overline{\beta }=0.30$ and $\overline{\dot{w}}=0$. (a) Limit cycles; (b) Time histories for different elastic moduli $\overline{E}$. As the elastic modulus $\overline{E}$ increases, the self-curling amplitude increases significantly, while the self-curling period is suppressed.

Figure 8

Effect of dimensionless gravitational acceleration on the self-curling of the LCE beam-mass system for the other parameters $\overline{H}=0.04$, $\overline{A}=0.36$, $\overline{E}=2.4$, ${\overline{I}}_0=0.06$, $\overline{\beta }=0.30$ and $\overline{\dot{w}}=0$. (a) Limit cycles; (b) Time histories for different gravitational accelerations $\overline{g}$. As the gravitational acceleration $\overline{g}$ increases, the self-curling amplitude exhibits a considerable decrease, and the self-curling period is suppressed. Figure 8 presents the effect of dimensionless gravitational acceleration on the self-curling of the LCE beam. In the calculation, we set the other parameters $\overline{H}=0.04$, $\overline{A}=0.36$, $\overline{E}=2.4$, ${\overline{I}}_0=0.06$, $\overline{\beta }=0.30$ and $\overline{\dot{w}}=0$.

Figure 9

Effect of dimensionless damping factor on the self-curling of the LCE beam-mass system for the other parameters $\overline{H}=0.04$, $\overline{A}=0.36$, $\overline{E}=2.4$, ${\overline{I}}_0=0.06$, $\overline{g}=0.015$ and $\overline{\dot{w}}=0$. (a) Limit cycles; (b) Time histories for different damping factors $\overline{\beta }$. As the damping factor $\overline{\beta }$ increases, the self-curling amplitude decreases significantly, while the self-curling period remains almost constant.