The Kelvin-Voigt visco-elastic model involving a fractional-order time derivative for modelling torsional oscillations of a complex discrete biodynamical system

Abstract

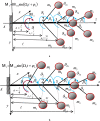
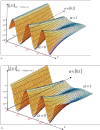
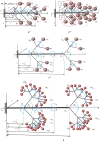
Under external loads trees exhibit complex oscillatory behaviour: their canopies twist and band. The great complexity of this oscillatory behaviour consists to an important degree of torsional oscillations. Using a system of ordinary differential fractional-order equations, free and forced main eigen-modes of fractional-type torsional oscillations of a hybrid discrete biodynamical system of complex structures were done. The biodynamical system considered here corresponds to a tree trunk with branches and is in the form of a visco-elastic cantilever of complex structure. Visco-elasticity corresponds to different ages of a tree. We set up a new model of torsional oscillations of a complex discrete, biodynamical system, using the Kelvin-Voigt visco-elastic model involving a fractional-order time derivative. The analytical expressions describing the characteristic properties of its fractional-type oscillations are determined. Based on mathematical and qualitative analogies, this concept represents a new model of torsional oscillations of a light cantilever that takes into account visco-elastic, dissipative properties of the material. Rigid discs are attached to the cantilever. Expressions for kinetic energy, deformation work and a generalized function of the fractional-type energy dissipation of this biodynamical system are defined. Independent main eigen-modes of the fractional type for free and forced torsional oscillations were determined for a special class of such systems, using formulas for the transformation of independent generalized angle coordinates to the principal main eigen-coordinates of the system. The forms of their approximate analytical solutions are shown. In the general case for inhomogeneous biodynamical systems of fractional type, there are no independent main fractional-type eigen-modes of torsional oscillations. The system behaves as a nonlinear system. A new constitutive relation between coupling of torsion loading to a visco-elastic fractional-type cantilever with fractional-type dissipation of cantilever mechanical energy and angle of torsion deformation is determined using a fractional-order derivative. The main advantages of the proposed model are the possibility to analyse torsional oscillations of more complex structures and the possibility to analyse complex cantilevers with different cross-sectional diameters.

Fig. 1

Two models of complex discrete biodynamical system on rigid light rods with mass particles rigidly fixed on basic visco-elastic cantilever for torsional oscillations: a. with three degrees of freedom, b. with four degrees of freedom. ${\vartheta }_{2u}$ and ${\vartheta }_{3u}$ are upper and ${\vartheta }_{2d}$ and ${\vartheta }_{3d}$ are down independent generalized coordinates at cross sections 2 and 3, respectively. In cross sections  1, $m_1=0$

Fig. 2

A graphical presentation of the complement eigen-mode of free torsional oscillations of the models of complex discrete biodynamical system for torsional oscillations: a. fractional-order cosine-like mode ${\left[{\xi }_s\left(t\right)\right]}_{Likecos\left({\omega }_{s}t+{\alpha }_s\right)}$ and b. its first derivative expressed by surfaces drown by series along time in the analytical approximations

Fig. 3

A graphical presentation of the complement fractional-type eigen-mode of free torsional oscillations of the models of complex discrete biodynamical system for torsional oscillations: a. fractional-type sine-like mode ${\left[{\xi }_s\left(t\right)\right]}_{Likesin\left({\omega }_{s}t+{\alpha }_s\right)}$ and b. its first derivative expressed by surfaces drown by series along time in the analytical approximations

Fig. 4

Fractal concept of hybrid biodynamical fractional-type system with complex discrete structure on visco-elastic fractional-type cantilever: a. basic version of the hybrid biodynamical model with discrete structure on visco-elastic fractional-type cantilever; b. hybrid model; c. details of the hybrid model; d. single discrete fractal chain–string structure