Generalised exponential-Gaussian distribution: a method for neural reaction time analysis

Abstract

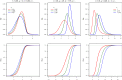
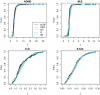
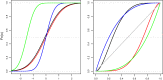
Reaction times (RTs) are an essential metric used for understanding the link between brain and behaviour. As research is reaffirming the tight coupling between neuronal and behavioural RTs, thorough statistical modelling of RT data is thus essential to enrich current theories and motivate novel findings. A statistical distribution is proposed herein that is able to model the complete RT's distribution, including location, scale and shape: the generalised-exponential-Gaussian (GEG) distribution. The GEG distribution enables shifting the attention from traditional means and standard deviations to the entire RT distribution. The mathematical properties of the GEG distribution are presented and investigated via simulations. Additionally, the GEG distribution is featured via four real-life data sets. Finally, we discuss how the proposed distribution can be used for regression analyses via generalised additive models for location, scale and shape (GAMLSS).

Keywords: Cognitive neuroscience; Exponential Gaussian distribution; Generalised additive models for location, Scale and shape; Neuronal response latency; Reaction times.

Fig. 1

Probability density (first row) and cumulative distribution functions (second row) for values of $\tau ,\mu ,\sigma$, and $\alpha$ of the GEG distribution. Three negatively skewed, symmetric, and positively skewed shapes are shown in the first, second, and third columns respectively

Fig. 2

Empirical CDFs of four real-life data sets and four fitted theoretical CDFs. The data distributions are represented by black dots (eCDF). Note that the NO distribution tends to miss the tails of the data (e.g. in data sets M.S. and C.D.) and in other cases it misses the data locations (e.g. in the C.D. data set). Note there is a trade-off between interpretability and fitness (i.e. accuracy and flexibility) that requires careful consideration when selecting a distribution to model data. GEG = four-parameters Generalised Exponential-Gaussian distribution; NO = two-parameter Normal distribution; G = two-parameter Gamma distribution; SN = three-parameter Skew-Normal distribution. The x axis represents RTs (these were divided by 100 to improve numerical stability). See Table 3 for the results of the fits

Fig. 3

Cumulative distribution functions (CDF) illustrating different normal (left plot) and non-normal distributions (right plot). Left plot (differences/similarities in location and scale): black and red CDFs have similar location and similar scale; blue and black/red CDFs have similar location and different scale; blue and green CDFs have different location and similar scale; green and black/red CDFs have different location and different scale. In all these cases, LM and GLM would be able to identify similarities/differences in location only (i.e. mean values); that is, standard techniques are good for detecting shifts but not shapes of distributions. Right plot (different types of shapes): black and blue CDFs represent distributions with positive skew, green and red CDFs represent distributions with negative skew, and the grey CDF represents a uniform distribution. The dotted grey horizontal line cuts through the distributions medians