Fundamental energy cost of finite-time parallelizable computing

Abstract

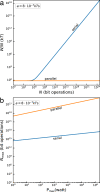
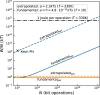
The fundamental energy cost of irreversible computing is given by the Landauer bound of [Formula: see text]/bit, where k is the Boltzmann constant and T is the temperature in Kelvin. However, this limit is only achievable for infinite-time processes. We here determine the fundamental energy cost of finite-time parallelizable computing within the framework of nonequilibrium thermodynamics. We apply these results to quantify the energetic advantage of parallel computing over serial computing. We find that the energy cost per operation of a parallel computer can be kept close to the Landauer limit even for large problem sizes, whereas that of a serial computer fundamentally diverges. We analyze, in particular, the effects of different degrees of parallelization and amounts of overhead, as well as the influence of non-ideal electronic hardware. We further discuss their implications in the context of current technology. Our findings provide a physical basis for the design of energy-efficient computers.

Fig. 1. Assumptions for ideal serial and parallel computers.

a Schematic illustration of the three main assumptions: (i) The total time $\mathcal{T}$ available to solve a given problem requiring N irreversible computing operations is limited; (ii) an ideal serial computer (left, blue) reduces the time per operation τ_s with increasing problem size N; (iii) an ideal parallel computer (right, red) is able to increase the number of processors n proportional to the size N in order to keep the time per operation τ_p constant. b Optimal 1/τ behavior of the energy consumption of a single algorithmic operation of duration τ, and the effects that the serial (blue) or parallel (red) computing strategies have on the energetic cost of computation.

Fig. 2. Finite-time Landauer bound for ideal serial and parallel computers.

a Energy consumption per operation, W/N, for solving a fully parallelizable problem of size N by an ideal serial, Eq. (3) (blue), and parallel, Eq. (4) (orange), computer. The energetic cost diverges with N for an ideal serial computer and remains constant for an ideal parallel computer. b Maximal number of bit operations $N_{\max }^{\mathrm{ser}}{N}_{\max }^{\mathrm{par}}$ that can be performed by an ideal serial, Eq. (5) (blue), and parallel, Eq. (6) (orange), computer in the finite time $\mathcal{T}=1$ s within a given power budget $P_{\max }$. Parameters are T = 1 K, b = 1 and a = 8⋅10⁻⁷kTs.

Fig. 3. Fundamental limit and extrapolated energy cost per operation for ideal serial and parallel computers.

Fundamental limits obtained for a = h (Planck constant; T = 1K) (solid lines) and extrapolated energy cost corresponding to a = 2.3kTs (Xeon Phi; T = 330 K) (dashed lines) for ideal serial, Eq. (3) (blue), and parallel, Eq. (4) (orange), computers. The measured value for a Xeon Phi processor is represented by a black X. For reference, an energy cost of 1 J/operation is shown as a dash-dotted line. Parameters are $\mathcal{T}=1$ s and b = 1.

Fig. 4. Effects of not ideally parallelizable problems.

a Energy cost per operation $W_{\mathrm{tot}}^{\mathrm{com}}/N$ for a partially parallelizable algorithm that has no overhead, Eq. (7). b Energy cost per operation $W_{\mathrm{tot}}^{\mathrm{ove}}/N$ for a fully parallel algorithm with linear overhead N_ove(n) = cn, Eq. (9), and c = 0 − 5000%. Same parameters as in Fig. 2.