Experimental insights into elasto-inertial transitions in Taylor-Couette flows

Abstract

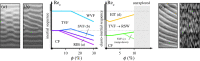
Since the seminal work of Taylor in 1923, Taylor-Couette (TC) flow has served as a paradigm to study hydrodynamic instabilities and bifurcation phenomena. Transitions of Newtonian TC flows to inertial turbulence have been extensively studied and are well understood, while in the past few years, there has been an increasing interest in TC flows of complex, viscoelastic fluids. The transitions to elastic turbulence (ET) or elasto-inertial turbulence (EIT) have revealed fascinating dynamics and flow states; depending on the rheological properties of the fluids, a broad spectrum of transitions has been reported, including rotating standing waves, flame patterns (FP), and diwhirls (DW). The nature of these transitions and the relationship between ET and EIT are not fully understood. In this review, we discuss experimental efforts on TC flows of viscoelastic fluids. We outline the experimental methods employed and the non-dimensional parameters of interest, followed by an overview of inertia, elasticity and elasto-inertia-driven transitions to turbulence and their modulation through shear thinning or particle suspensions. The published experimental data are collated, and a map of flow transitions to EIT as a function of the key fluid parameters is provided, alongside perspectives for the future work. This article is part of the theme issue 'Taylor-Couette and related flows on the centennial of Taylor's seminal Philosophical Transactions paper (part 1)'.

Keywords: Taylor–Couette flow; elasto-inertia; experiments.

Figure 1.

A map of flow states for co-rotating and counter-rotating TC flow in the Newtonian case (($a$) derived from [14], elastic number $\mathrm{El}=0$) and in a viscoelastic case (($b$) derived from [15], elastic number $\mathrm{El}\simeq 0.1$–$0.2$) for inner and outer cylinder Reynolds number, Re${\hspace{0.17em}}_i\in [0:300]$ and Re${\hspace{0.17em}}_o\in [-150:150]$, respectively. Those illustrate the two very different populations of expected flow states. Acronyms for flow states are defined later in the text. (Online version in colour.)

Figure 2.

Schematic representation of common experimental techniques used to investigate TC flows. ($a,b$) Planar laser-induced fluorescence (PLIF) is used to assess mixing performances (e.g. [42,43]); flow vislualization allows us to easily probe the flow structure and construct spatio-temporal diagrams (e.g. [15,23,44,45]); torque measurement can detect the onset of secondary flows and evaluate friction properties of flow states [–48]; particle image velocimetry (PIV) is designed to measure flow velocity and accurately describe flow features within the gap (e.g. [49]); alternatively, qualitative in-plane visualization can be performed using rheoscopic flakes similar to the ones employed for the spatio-temporal analysis [–52]; laser Doppler velocimetry (LDV) is used to measure fluid velocity locally with a high temporal resolution [53]. (Online version in colour.)

Figure 3.

Illustration of key rheological characterization for the study of elasto-inertial TC flow. (a) Steady-shear characterization of potentially shear-rate dependent dynamic viscosity, from which an estimate of the elastic time scale can be occasionally derived (see the works of [45,66]). (b) Steady-shear characterization of the first normal stress difference as a way to estimate $t_e$ [52,67]. (c) Small amplitude oscillatory shear testing where the elastic time scale is estimated from the loss ($G^{\mathrm{\prime }\mathrm{\prime }}$) and elastic ($G^{\prime }$) moduli curves as in [23,44,68,69]. (d) Filament thinning tests typically performed on CaBER rheometers relating the elastic time scale to the dynamics of an elongated filament, as used in [15,47] among others. (Online version in colour.)

Figure 4.

Sketches of various flow states encountered during inertial and elasto-inertial transition sequences. All images are space-time diagrams (with time on the $x$-axis and the axial distance on the $y$-axis) constructed from flow visualization, and represent steady-state cases for which the control parameters were constant. Illustrations were taken from [23,45,47,69,81]. (Online version in colour.)

Figure 5.

Illustration of the modulation of EIT by shear thinning, inspired and adapted from [23,47,68,138]. (Online version in colour.)

Figure 6.

Simplified representation of the inertial ($a,b$) and elasto-inertial ($c,d$) transition sequences in particle loaded fluids. Images shown in $a,b$ are inspired from [48,85,143] among others and show that particles destabilize first- and second-order flow states. RIB and SVF states are illustrated by images extracted from [143] and rescaled (a,b). Images shown in (c,d) are inspired from [146] and shows that, on a smaller particle volume fraction range explored, particles on the other hand tend to stabilize elasto-inertial flow states. (Online version in colour.)

Figure 7.

Elasticity number—viscosity ratios as extracted from the literature. Circles denote Newtonian transitions characterized by variations of the CF$\to$TVF$\to$WTVF pathway, squares denote moderately elastic transitions for Boger fluids incorporating CF$\to$TVF$\to$RSW$\to$MST$\to$EIT as a basic path and diamonds correspond to highly elastic transitions with FP, following CF$\to$RSW$\to$FP$\to$EIT. Black markers correspond to Boger fluids, blue markers to shear-thinning fluids and cyan markers to highly elastic-highly shear-thinning cases. ED is the elasticity-dominated regime, ID is the inertia-dominated regime and INT is the intermediate regime. (Online version in colour.)