Memorizing without overfitting: Bias, variance, and interpolation in overparameterized models
- PMID: 36713351
- PMCID: PMC9879296
- DOI: 10.1103/physrevresearch.4.013201
Memorizing without overfitting: Bias, variance, and interpolation in overparameterized models
Abstract
The bias-variance trade-off is a central concept in supervised learning. In classical statistics, increasing the complexity of a model (e.g., number of parameters) reduces bias but also increases variance. Until recently, it was commonly believed that optimal performance is achieved at intermediate model complexities which strike a balance between bias and variance. Modern Deep Learning methods flout this dogma, achieving state-of-the-art performance using "over-parameterized models" where the number of fit parameters is large enough to perfectly fit the training data. As a result, understanding bias and variance in over-parameterized models has emerged as a fundamental problem in machine learning. Here, we use methods from statistical physics to derive analytic expressions for bias and variance in two minimal models of over-parameterization (linear regression and two-layer neural networks with nonlinear data distributions), allowing us to disentangle properties stemming from the model architecture and random sampling of data. In both models, increasing the number of fit parameters leads to a phase transition where the training error goes to zero and the test error diverges as a result of the variance (while the bias remains finite). Beyond this threshold, the test error of the two-layer neural network decreases due to a monotonic decrease in both the bias and variance in contrast with the classical bias-variance trade-off. We also show that in contrast with classical intuition, over-parameterized models can overfit even in the absence of noise and exhibit bias even if the student and teacher models match. We synthesize these results to construct a holistic understanding of generalization error and the bias-variance trade-off in over-parameterized models and relate our results to random matrix theory.
Figures
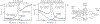



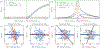
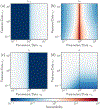
References
-
- Lecun Yann, Bengio Yoshua, and Hinton Geoffrey, “Deep learning,” Nature 521, 436–444 (2015). - PubMed
-
- Canziani Alfredo, Paszke Adam, and Culurciello Eugenio, “An Analysis of Deep Neural Network Models for Practical Applications,” (2017), arXiv:1605.07678.
-
- Zhang Chiyuan, Bengio Samy, Hardt Moritz, Recht Benjamin, and Vinyals Oriol, “Understanding Deep Learning Requires Re-thinking Generalization,” International Conference on Learning Representations (ICLR) (2017).
-
- “See supplemental material at [url] for complete analytic derivations and additional numerical results.”.
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
