Fluctuations in pedestrian dynamics routing choices

Abstract

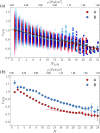
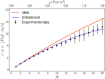
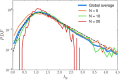
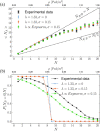
Routing choices of walking pedestrians in geometrically complex environments are regulated by the interplay of a multitude of factors such as local crowding, (estimated) time to destination, and (perceived) comfort. As individual choices combine, macroscopic traffic flow patterns emerge. Understanding the physical mechanisms yielding macroscopic traffic distributions in environments with complex geometries is an outstanding scientific challenge, with implications in the design and management of crowded pedestrian facilities. In this work, we analyze, by means of extensive real-life pedestrian tracking data, unidirectional flow dynamics in an asymmetric setting, as a prototype for many common complex geometries. Our environment is composed of a main walkway and a slightly longer detour. Our measurements have been collected during a dedicated high-accuracy pedestrian tracking campaign held in Eindhoven (The Netherlands). We show that the dynamics can be quantitatively modeled by introducing a collective discomfort function, and that fluctuations on the behavior of single individuals are crucial to correctly recover the global statistical behavior. Notably, the observed traffic split substantially departs from an optimal, transport-wise, partition, as the global pedestrian throughput is not maximized.

Keywords: collective behavior; fluctuations; high-statistics pedestrian dynamics; pedestrians routing; stochastic variational principle.

Fig. 1.

Overview of the experimental data. In (a) and (b) we show two examples of overhead frames recorded by the depth cameras. The depth field in (a) depicts a set of N = N_A = 13 pedestrians all taking the straight path (path A), while in (b) we provide an example of a more balanced pedestrian distribution. The gray shades represent the distance between each pixel and the camera plane (i.e. the elevation from the ground). This type of data allows reliable pedestrian tracking (see “Materials and methods” for details). The automatic tracking output is overlayed as solid colored lines. (c) Heat-map of pedestrians position from the entire dataset. We remark that the colorbar is given in logarithmic scale. The streamlines of the (spatially binned) mean velocity vector are used in order to provide a visual representation of the most probable trajectories.

Fig. 2.

Experimental setup from the viewpoint of a pedestrian walking towards the path bifurcation (a) and sketch of the floor plan (b). A low-fence blockage drives the pedestrian flow towards one same entrance point, while a set of bollards separates the bicycle lane from the adjacent road preventing pedestrians from entering the system from other locations or to exit by an area not covered by cameras. A grid of 4×2 Orbbec depth cameras, hanging below the overpass connecting the Philips Stadium to a nearby train station, is used to collect trajectories within the area marked by dotted black lines in (b).

Fig. 3.

Average number of people taking path A (〈N_A〉, red dots) and B (〈N_B〉, blue dots) as a function of the global pedestrian count N. We observe that until N < N* = 10, on average less than one person opts to travel along path B. Above the N* threshold, people start making systematic use of path B and both diagrams exhibit a clear change. The blue colorbars provide a visual representation of the probability distribution P(N_B|N) of number of people taking path B, conditioned to the global pedestrian count N. Even when N > N*, configurations in which no pedestrian walks on path B are frequent.

Fig. 4.

Fundamental velocity diagrams. (a) Local velocity as a function of the number of people present along path A (red) and path B (blue). Dots represent the average values, while colorbars synthesize the probability distribution functions (PDFs). The black solid line provides a linear fit of the local velocity diagrams under the reasonable assumption that the same fundamental diagram applies to both paths. (b) Global velocity as function of the total number of people in the system. We highlight an evident change in the slope of the diagram for both path A and path B for N > N*, which we model (dotted lines) with a re-parametrization of the local velocity diagram. (See main text for details).

Fig. 5.

Average pedestrian flow (Eq. 8) as a function of the pedestrian count. The solid lines represent the theoretical maximum (orange color) and minimum (purple color) case scenarios. We observe that experimental results (black dots) on average closely follow the flow of the most unbalanced case. The error bars have been obtained by dividing the data into 10 bins, with the extrema of the error bars representing the minimum and maximum average value per bin.

Fig. 6.

PDF of the perceived path length ratio λ_p [cf. (18)]. We report the distribution for for three different global density values, respectively at low (N = 5), intermediate (N = 10), and high (N = 20) density values. The blue line shows the PDF obtained considering the overall dataset, with the black dotted line representing a fit making use of an exponentially modified Gaussian (see Eq. 20), with mean μ = 0.77 and standard deviation σ = 0.30, and an exponential distribution with scale parameter β = 0.68.

Fig. 7.

Comparison of numerical results from simulations against experimental data. (a) <N_A(N)>: the average number of people taking path A as a function of the global pedestrian count N. (b) P(N_B = 0|N), the Bernoulli probability of observing configurations in which no pedestrians walk across path B, conditioned on the global pedestrian count N. It is evident that fluctuations on the perceived path length allow a more realistic description of the transition around N*, as shown in (b), still correctly capturing the average behavior, as shown in (a).

Fig. 8.

PDF of number of people in path B, N_B, conditioned on the global count N. We report three examples, representative of three different levels of density: from left to right N = 5, 10, and 15, respectively. The experimental data (black bars) are compared against the results obtained employing three different models: in blue; the results obtained employing a deterministic model in which individual fluctuations are neglected, in orange; the results of a stochastic model accounting for fluctuations in individuals free-stream velocities, and finally, in green; the results of a stochastic model accounting for fluctuations in both free-stream velocities and path length perception for single individuals.