Optimizing NV magnetometry for Magnetoneurography and Magnetomyography applications

Abstract

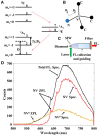
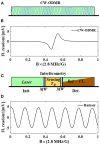
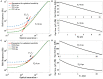
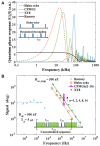
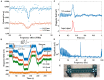
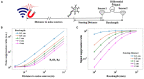
Magnetometers based on color centers in diamond are setting new frontiers for sensing capabilities due to their combined extraordinary performances in sensitivity, bandwidth, dynamic range, and spatial resolution, with stable operability in a wide range of conditions ranging from room to low temperatures. This has allowed for its wide range of applications, from biology and chemical studies to industrial applications. Among the many, sensing of bio-magnetic fields from muscular and neurophysiology has been one of the most attractive applications for NV magnetometry due to its compact and proximal sensing capability. Although SQUID magnetometers and optically pumped magnetometers (OPM) have made huge progress in Magnetomyography (MMG) and Magnetoneurography (MNG), exploring the same with NV magnetometry is scant at best. Given the room temperature operability and gradiometric applications of the NV magnetometer, it could be highly sensitive in the $\text{pT}/\sqrt{\text{Hz}}$ -range even without magnetic shielding, bringing it close to industrial applications. The presented work here elaborates on the performance metrics of these magnetometers to the state-of-the-art techniques by analyzing the sensitivity, dynamic range, and bandwidth, and discusses the potential benefits of using NV magnetometers for MMG and MNG applications.

Keywords: MMG; MNG; bandwidth; dynamic range; magnetometer; nitrogen-vacancy center; sensitivity.

Figure 1

(A) Energy level diagram of negatively charged NV center in diamond. The bias field B₀ degenerate the m_s = ±1 states by 2γ_eB₀. The zero-field splitting is D ≈ 2.87 GHz. The numbers are used to label the different levels. (B) Structure of NV center in diamond. The applied B₀ field is parallel to the N-V orientation, and the applied driving field B₁ is supposed to be perpendicular to the N-V axis. (C) A typical setup of the NV magnetometer. The green laser is illuminated on the diamond, which is assembled with the optics to collect and guide the fluorescences for detection. The microwave field is used for resonant driving of the spin states. (D) Fluorescence spectrum (the highest black line) emitted by NV center ensembles in a 0.5³mm³ diamond. The signals from the two different charge states, i.e., NV⁻ (the middle red line) and NV⁰ (the lowest yellow line) centers, are estimated in the figure.

Figure 2

(A) CW-ODMR method uses continuous wave laser pumping and MW field driving. The MW field is modulated in frequency or phase to get a modulated fluorescence signal. (B) CW-ODMR spectrum demodulated by the lock-in amplifier. MW frequency shift is used to simulate the line shift induced by an external field. B × (2.8 MHz/G) is used as the description of the horizontal axis to show the relationship between the external field (in Gauss) and the line shift (in MHz). (C) Most of the interferometry methods consists of three parts, i.e., initialization, sensing, and detection. In the initialization part, a green laser (532 nm) is used to polarize spin states into m_s = 0, regardless of the fluorescence emitted from the diamond. In the sensing part, the two blue blocks represent two MW pulses in a Ramsey sequence, and the yellow block depicts the magnetic field sensing time. The Ramsey sequence can be replaced by different interferometry sequences to measure dc/ac magnetic fields. In the detection part, fluorescences are collected to readout the spin population which indicates the spin-detected magnetic field information. The wedge red indicates that the fluorescence drops at the beginning of the detection window and continuously increases due to the repolarization induced by the detection-laser pulse. (D) The sensor response of Ramsey measurement to the MW frequency shift, which is equivalent to the response to the magnetic field.

Figure 3

(A) Optimization of parameters for the sensitivity of CW-ODMR NV-magnetometry. The three curves (dash, dot, and dash-dot) indicate the Rabi frequencies for the optimized sensitivities with different laser powers. The different curves use different $T_2^{*}$ for the calculations. The solid line plots both the laser powers and the Rabi frequencies of the optimized sensitivities for different $T_2^{*}$, and the dots are the crossing spots with the other three curves. (B) The upper graph shows that the optimal Rabi frequency is logarithmically linear to the $T_2^{*}$ of the diamond. The lower graph shows that the calculated optimized sensitivity is also logarithmically linear to the $T_2^{*}$. (C) Optimization of parameters for sensitivities of diamonds with different T₁. The curves for different T₁ are calculated with $T_2^{*}=2\mu s$. The solid line indicates the parameters for optimized sensitivity with different T₁. (D) The upper graph shows the relationship of the optimal Rabi frequency for different T₁, and the lower graph shows the best sensitivities that can be achieved by the diamonds with different T₁.

Figure 4

(A) Filter functions of different pulsed sequences that can be used in NV-magnetometry. In the calculation of the filter function of the Ramsey sequence, the sensing time T_ϕ = 6.5μs. In the calculations of the sequences for ac field sensing, i.e., Hahn-echo, CPMG2, and XY8, the sensing time T_ϕ = 50μs. (B) An overview of the measured frequency responses of NV-magnetometry using the different sequences. The QPSD technique is used to read out the field strength by extracting the quantum phase measured by the sequences. The “×” shows the response of the Ramsey sequence, of which the bandwidth is limited by the sampling rate in the experiment. The “+” and the “◦” shows the ac field responses regarding different T_ϕ when Hahn-echo and XY8 are applied for the measurements. The “△” shows the measurements of a 200 kHz signal by CPMG sequences with different numbers of the π-pulses. One of the primary goals of the NV-magnetometry development is to develop concatenation of the sequences that can ensure a flat frequency response for ac field sensing.

Figure 5

(A) ODMR spectra with different local gradients at the diamond. (B) Magnetic field detected by the NV gradiometer in the unshielded environment with the comparison of a fluxgate magnetometer. The schematic of the setup is shown as the inset drawing. The step signals are generated by an elevator nearby. From top to bottom, the lines are signals from the fluxgate sensor, NV gradiometer channel 1 and channel 2, and the output of the NV gradiometer, i.e., subtraction of the two channels. The dashed lines and arrows are the eye-guide for comparing the noise of NV channels and the fluxgate magnetometer. (C) The action potential signal (generated by a phantom) detected by the NV magnetometer. The original input of the action potential is as the lower waveform shows. The detected magnetic field amplitude is about 2 nT. (D) is the Fourier transform of the detected action potential signal. The principle noise peaks are at dc, 50 Hz, and 100 Hz. (E) The phantom used for generating magnetic field signals to simulate the MMG signal.

Figure 6

(A) Sketch of relevant parameters that have to be taken into account when compromising the noise and signal suppression in a linear gradiometer configuration. (B) Noise suppression ratio for different baselengths as a function of the distance to the noise sources. (C) Relative differential signal of the gradiometers for different distances to the signal source as a function of baselength. For both cases, it is assumed that the magnetic field strength of the noise source and signal sources decay as B(r) ∝ r⁻² with distance to the different sources.

Figure 7

(A) For a cube-shaped muscle compound, muscle action potentials are simulated when muscle fibers in different depths are stimulated. A 2 mm thick fat tissue layer is added on top of the muscle, and the magnetic field is observed midway between the innervation zone (IZ) and the myotendinous junction (MTJ). For obtaining a differential signal, the magnetic field is sampled at the body surface and in a line with distance $\Delta x_{\text{t}}^{\perp }$ above the muscle surface. (B) Exemplary MMG signal measured at one point with a distance of 0.5 mm to the body surface when varying the depth of the active muscle fibers. (C) Signal amplitude on the body surface in a line perpendicular to the muscle fibers (cf. A). The left column shows the root mean square (RMS) of the raw MMG signal, depending on the spatial coordinate and the depth of the active muscle fibers. The middle and the right column show the RMS distribution corresponding to differential signals with inter-sensor distances of 5 and 0.5 mm, respectively. Thereby, it can be observed that decreasing the distance between the sensors narrows the amplitude distributions and hence reduces the detection volume of measurement.