Statistical shape modeling of multi-organ anatomies with shared boundaries

Abstract

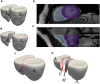
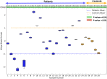
Introduction: Statistical shape modeling (SSM) is a valuable and powerful tool to generate a detailed representation of complex anatomy that enables quantitative analysis of shapes and their variations. SSM applies mathematics, statistics, and computing to parse the shape into some quantitative representation (such as correspondence points or landmarks) which can be used to study the covariance patterns of the shapes and answer various questions about the anatomical variations across the population. Complex anatomical structures have many diverse parts with varying interactions or intricate architecture. For example, the heart is a four-chambered organ with several shared boundaries between chambers. Subtle shape changes within the shared boundaries of the heart can indicate potential pathologic changes such as right ventricular overload. Early detection and robust quantification could provide insight into ideal treatment techniques and intervention timing. However, existing SSM methods do not explicitly handle shared boundaries which aid in a better understanding of the anatomy of interest. If shared boundaries are not explicitly modeled, it restricts the capability of the shape model to identify the pathological shape changes occurring at the shared boundary. Hence, this paper presents a general and flexible data-driven approach for building statistical shape models of multi-organ anatomies with shared boundaries that explicitly model contact surfaces. Methods: This work focuses on particle-based shape modeling (PSM), a state-of-art SSM approach for building shape models by optimizing the position of correspondence particles. The proposed PSM strategy for handling shared boundaries entails (a) detecting and extracting the shared boundary surface and contour (outline of the surface mesh/isoline) of the meshes of the two organs, (b) followed by a formulation for a correspondence-based optimization algorithm to build a multi-organ anatomy statistical shape model that captures morphological and alignment changes of individual organs and their shared boundary surfaces throughout the population. Results: We demonstrate the shared boundary pipeline using a toy dataset of parameterized shapes and a clinical dataset of the biventricular heart models. The shared boundary model for the cardiac biventricular data achieves consistent parameterization of the shared surface (interventricular septum) and identifies the curvature of the interventricular septum as pathological shape differences.

Keywords: biventricular cardiac MRI; interventricular septum; particle-based shape modeling; shared boundaries; statistical shape modeling.

FIGURE 1

Extracting shared boundary between two meshes. The regions in green have Euclidean distances that fall within the threshold and are extracted as a shared boundary as per step 2. The green arrows show the distances within the threshold for the vertices included in the shared boundary. The red arrows show distances greater than the threshold for the vertices excluded from the shared boundary. The contour is extracted from the green region as per step 4. Note: the meshes are farther apart, and the threshold is larger for visualization purposes.

FIGURE 2

An example of output obtained after shared boundary extraction. Meshes representing (A) RV and LVW show that they have a shared boundary surface, and (B) RV and LVW meshes are pried apart. The meshes and contour obtained after shared boundary extraction (C) RV, LVW, shared surface and contour (D) all outputs pried apart for visualization. The red color indicates the contour. The image shows 2D slices of the endocardial segmentation for the RV (blue) and epicardial segmentation for the LV (violet) at end-diastole in the (E) axial view and (F) coronal view.

FIGURE 3

Synthetic Peanut Dataset: Surface meshes representing the two groups included in the peanut dataset- (A) Controls group: two spheres with varying radii, (B) pathalogical changes are emulated by changing one of the spheres to ellipsoid. (C) Samples from the controls and pathalogy groups show casing the shared boundary surface, (D) sample outputs obtained after extracting the shared boundary surface and contour. The meshes are pried apart for visualization.

FIGURE 4

(A) Two viewpoints of the point distribution models and the reconstructed meshes of the modes of variations of the peanut dataset discovered by the shared boundary model. (B) Group-level shape differences observed by the shared boundary shape model. The arrows indicate the direction of shape change, the yellow mesh represents the extracted shared boundary, and the white represents one of the shapes of the peanut.

FIGURE 5

Two different views of the same reconstructed meshes and the point distribution models of the modes of variations discovered by (A) multiple domains model and (B) the proposed shared boundary model. The red boxes indicate shape modeling inconsistencies of multiple domain model - particle overlap and gaps between organs. (C) Examples of shapes with overlapping particles and shapes with gaps between organs in the multiple domains model and (D) examples of shapes with consistent parameterization in the proposed shared boundary model.

FIGURE 6

Group shape differences identified by (A) the proposed shared boundary and (B) the multiple domains model. Each row shows the samples from a different view to visualize the differences. The black arrows indicate the direction of the variation of shape.

FIGURE 7

Alignment variations identified using multi-level component analysis for the cardiac dataset. The surface meshes in yellow represent the mean reconstructed shape, and the surface meshes in red represent the shapes at μ+2σ and μ−2σ. The black arrows indicate the direction of the variation of the pose.

FIGURE 8

Shape variations identified using multi-level analysis for the cardiac dataset visualized from two different views.

FIGURE 9

The box whisker plot shows the distribution of the shape-based scores for each sample from ten different shape models generated to study the effect of data imbalance. The table at the top of the plot shows the p-values of the shape-based scores.