Crucial 3-D viscous hydrodynamic contributions to the theoretical modeling of the cochlear response

Abstract

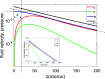
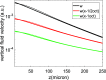
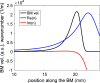
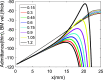
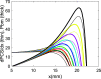
This study uses a 3-D representation of the cochlear fluid to extend the results of a recent paper [Sisto, Belardinelli, and Moleti (2021b). J. Acoust. Soc. Am. 150, 4283-4296] in which two hydrodynamic effects, pressure focusing and viscous damping of the BM motion, both associated with the sharp increase in the wavenumber in the peak region, were analyzed for a 2-D fluid, coupled to a standard 1-D transmission-line WKB approach to cochlear modeling. The propagation equation is obtained from a 3-D fluid volume conservation equation, yielding the focusing effect, and the effect of viscosity is represented as a correction to the local 1-D admittance. In particular, pressure focusing amplifies the BM response without modifying the peak admittance, and viscous damping determines the position of the response peak counteracting focusing, as sharp gradients of the velocity field develop. The full 3-D WKB formalism is necessary to represent satisfactorily the behavior of the fluid velocity field near the BM-fluid interface, strictly related to viscous losses. As in finite element models, a thin layer of fluid is effectively attached to the BM due to viscosity, and the viscous force associated with the vertical gradient of the fluid vertical velocity acts on the BM through this layer.

FIG. 1.

Schematic representation of the 3-D box model. The gray surface, with the small hole (helicotrema) at its apical end, represents the BM, which separates two symmetrical rectangular parallelepipedal scalae of height H, length L, and width W.

FIG. 2.

(Color online) Vertical profile of pressure and of the fluid velocity components (both in arbitrary units) near the BM in the 3-D WKB model, at the BP of the stimulus frequency f₀ = 2200 Hz, for G = 1.2. In the small picture, the same plot is extended over the whole height of the scala.

FIG. 3.

(Color online) Vertical profile of the vertical fluid velocity w, computed by the model (thin lines) and estimated from the pressure gradient (thick lines) at the BP and at two basal places corresponding to frequency shifts of a half octave and one octave. The semilogarithmic representation shows the approximately exponential vertical drop-off, which is not in agreement with the experimental power-law behavior of the Olson (1999) data.

FIG. 4.

(Color online) Vertical profile of the scalar (red) and vector (green) potential contributions to the total (blue) vertical gradient of the vertical fluid velocity component. This gradient peaks at d, and the narrow layer of thickness d is practically integral to the BM and follows its vertical motion. At z = 0 this gradient is null, because the scalar and vector potentials yield contributions of opposite phase.

FIG. 5.

(Color online) Real and imaginary parts of the wavenumber in the peak region, for a strongly active model (G = 1.2), along with the BM response profile (black), in arbitrary linear units. At the peak of the BM response the wave vector is still almost fully real-valued (and even not yet maximal), because the dependence on the wavenumber of the viscous damping causes a sharp decrease in the BM response well before the TW reaches the “nominal” resonant place, where the imaginary part of the wavenumber is largest. The green line shows the real part of β₀, associated with the vertical decay length of the rotational contributions to the velocity field, and reciprocal to the thickness d of the fluid layer that is effectively attached to the BM.

FIG. 6.

(Color online) Admittance (thin lines) and BM response (thick lines), in arbitrary dB units, for a set of increasingly active models, with G variable between 0.15 and 1.2, with 0.15 steps. In the peak region, the admittance is mostly real-valued.

FIG. 7.

(Color online) Comparison between the dissipation at the BM-fluid interface (thick lines) and the cross section integrated viscous dissipation per unit length (thin lines), in arbitrary dB units, for the eight increasingly active models of Fig. 6.