Modeling Syphilis and HIV Coinfection: A Case Study in the USA

Abstract

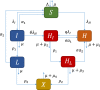
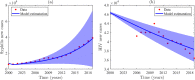
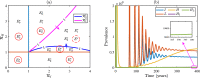
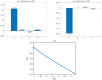
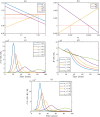
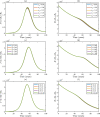
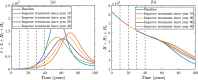
Syphilis and HIV infections form a dangerous combination. In this paper, we propose an epidemic model of HIV-syphilis coinfection. The model always has a unique disease-free equilibrium, which is stable when both reproduction numbers of syphilis and HIV are less than 1. If the reproduction number of syphilis (HIV) is greater than 1, there exists a unique boundary equilibrium of syphilis (HIV), which is locally stable if the invasion number of HIV (syphilis) is less than 1. Coexistence equilibrium exists and is stable when all reproduction numbers and invasion numbers are greater than 1. Using data of syphilis cases and HIV cases from the US, we estimated that both reproduction numbers for syphilis and HIV are slightly greater than 1, and the boundary equilibrium of syphilis is stable. In addition, we observed competition between the two diseases. Treatment for primary syphilis is more important in mitigating the transmission of syphilis. However, it might lead to increase of HIV cases. The results derived here could be adapted to other multi-disease scenarios in other regions.

Keywords: Coinfection; Epidemic model; HIV transmission; Invasion numbers; Reproduction numbers; Syphilis infection.

Fig. 1

Flow diagram of the model (1) (Color figure online)

Fig. 2

Model calibration by new primary and secondary syphilis cases and HIV cases in the US. The results for syphilis infection and HIV infection are shown in (a) and (b), respectively. The shaded regions are 95% confidence intervals. The data set used here is listed in Table 2 (Color figure online)

Fig. 3

a The existence and stability of the equilibrium of model (4) with different values of ${\mathcal{R}}_I$, ${\mathcal{R}}_H$, ${\mathcal{R}}_2^1$ and ${\mathcal{R}}_1^2$. The circled equilibrium is stable in each region. The dashed circle indicates that it is only numerically verified. The arrows represent that the corresponding invasion number changes from less that 1 to greater that 1. b The prevalence when ${\mathcal{R}}_I=2.18$, ${\mathcal{R}}_H=2.02$, ${\mathcal{R}}_2^1=1.03$, ${\mathcal{R}}_1^2=1.15$. Here $c_2=7.33\times {10}^5$ and $d_2=1.07\times {10}^6$. It shows that the coexistence equilibrium exists and is stable when ${\mathcal{R}}_I>1$, ${\mathcal{R}}_H>1$, ${\mathcal{R}}_2^1>1$ and ${\mathcal{R}}_1^2>1$, even when $c_2<d_2$ (Color figure online)

Fig. 4

a, b Elasticity indices of ${\mathcal{R}}_2^1$ and ${\mathcal{R}}_1^2$ with respect to parameters related to treatment and education. Parameter values are from Table 4. c The relation between ${\mathcal{R}}_2^1$ and ${\mathcal{R}}_1^2$. Here we vary ${\alpha }_1$ and the other parameter values are from Table 4 (Color figure online)

Fig. 5

a Reproduction numbers and invasion numbers given different values of ${\alpha }_1$. b Zoomed-in invasion numbers from (a). c–e Total syphilis infections, total HIV infections and total infections of two diseases respectively given different values of ${\alpha }_1$. In all panels, the other parameter values are from Table 4 (Color figure online)

Fig. 6

Total syphilis infections and total HIV infections respectively given different values of ${\alpha }_2$ (a, b), q (c, d), and $\theta$ (e, f). In all panels, the other parameter values are from Table 4 (Color figure online)

Fig. 7

Total syphilis infections (a) and total HIV infections (b) respectively given different starting years of the treatment improvement. In both panels, baseline corresponds to ${\alpha }_1=2.53$ and treatment improvement corresponds to ${\alpha }_1=2.58$. The other parameter values are from Table 4 (Color figure online)