Almost positive links are strongly quasipositive
- PMID: 36744241
- PMCID: PMC9889511
- DOI: 10.1007/s00208-021-02328-x
Almost positive links are strongly quasipositive
Abstract
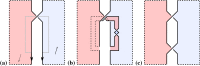
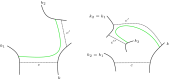
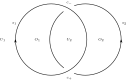
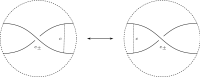
We prove that any link admitting a diagram with a single negative crossing is strongly quasipositive. This answers a question of Stoimenow's in the (strong) positive. As a second main result, we give a simple and complete characterization of link diagrams with quasipositive canonical surface (the surface produced by Seifert's algorithm). As applications, we determine which prime knots up to 13 crossings are strongly quasipositive, and we confirm the following conjecture for knots that have a canonical surface realizing their genus: a knot is strongly quasipositive if and only if the Bennequin inequality is an equality.
Keywords: 57M25.
© The Author(s) 2022.
Conflict of interest statement
Conflict of interestOn behalf of all authors, the corresponding author states that there is no conflict of interest and there is no further data.
Figures


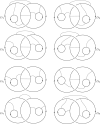
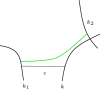

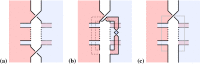
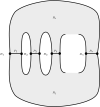
References
-
- Baader S. Quasipositivity and homogeneity. Math. Proc. Camb. Philos. Soc. 2005;139(2):287–290. doi: 10.1017/S0305004105008698. - DOI
-
- Baader S. Slice and Gordian numbers of track knots. Osaka J. Math. 2005;42:257–271.
-
- Baader S, Ishikawa M. Legendrian graphs and quasipositive diagrams. Ann. Fac. Sci. Toulouse Math. (6) 2009;18(2):285–305. doi: 10.5802/afst.1207. - DOI
-
- Baader S, Ishikawa M. Legendrian framings for two-bridge links. Proc. Am. Math. Soc. 2011;139(12):4513–4520. doi: 10.1090/S0002-9939-2011-10888-8. - DOI
-
- Bennequin D. Entrelacements et équations de Pfaff. Astérisque. 1983;107–108:87–161.
LinkOut - more resources
Full Text Sources
Research Materials
