Extra-axonal contribution to double diffusion encoding-based pore size estimates in the corticospinal tract
- PMID: 36745290
- PMCID: PMC10468962
- DOI: 10.1007/s10334-022-01058-8
Extra-axonal contribution to double diffusion encoding-based pore size estimates in the corticospinal tract
Abstract
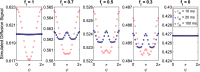
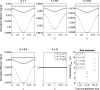
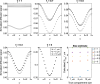
Objective: To study the origin of compartment size overestimation in double diffusion encoding MRI (DDE) in vivo experiments in the human corticospinal tract. Here, the extracellular space is hypothesized to be the origin of the DDE signal. By exploiting the DDE sensitivity to pore shape, it could be possible to identify the origin of the measured signal. The signal difference between parallel and perpendicular diffusion gradient orientation can indicate if a compartment is regular or eccentric in shape. As extracellular space can be considered an eccentric compartment, a positive difference would mean a high contribution to the compartment size estimates.
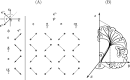
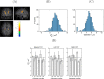
Materials and methods: Computer simulations using MISST and in vivo experiments in eight healthy volunteers were performed. DDE experiments using a double spin-echo preparation with eight perpendicular directions were measured in vivo. The difference between parallel and perpendicular gradient orientations was analyzed using a Wilcoxon signed-rank test and a Mann-Whitney U test.
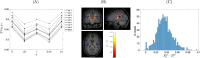
Results: Simulations and MR experiments showed a statistically significant difference between parallel and perpendicular diffusion gradient orientation signals ([Formula: see text]).
Conclusion: The results suggest that the DDE-based size estimate may be considerably influenced by the extra-axonal compartment. However, the experimental results are also consistent with purely intra-axonal contributions in combination with a large fiber orientation dispersion.
Keywords: Diffusion anisotropy; Extracellular space; Microstructure; Multiple wave vector diffusion weighting; Size estimates; White matter.
© 2023. The Author(s).
Conflict of interest statement
The authors declare no conflict of interest.
Figures

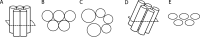





References
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

