Bottom-Up Informed and Iteratively Optimized Coarse-Grained Non-Markovian Water Models with Accurate Dynamics

Abstract

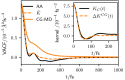
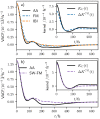
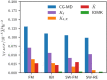
Molecular dynamics (MD) simulations based on coarse-grained (CG) particle models of molecular liquids generally predict accelerated dynamics and misrepresent the time scales for molecular vibrations and diffusive motions. The parametrization of Generalized Langevin Equation (GLE) thermostats based on the microscopic dynamics of the fine-grained model provides a promising route to address this issue, in conjunction with the conservative interactions of the CG model obtained with standard coarse graining methods, such as iterative Boltzmann inversion, force matching, or relative entropy minimization. We report the application of a recently introduced bottom-up dynamic coarse graining method, based on the Mori-Zwanzig formalism, which provides accurate estimates of isotropic GLE memory kernels for several CG models of liquid water. We demonstrate that, with an additional iterative optimization of the memory kernels (IOMK) for the CG water models based on a practical iterative optimization technique, the velocity autocorrelation function of liquid water can be represented very accurately within a few iterations. By considering the distinct Van Hove function, we demonstrate that, with the presented methods, an accurate representation of structural relaxation can be achieved. We consider several distinct CG potentials to study how the choice of the CG potential affects the performance of bottom-up informed and iteratively optimized models.

Figure 1

VACFs of the IBI water model, parametrized with K̃(t) (eq 15) calculated based on the BOD method, compared to the AA reference. For comparison we also show the result of nondissipative CG-MD simulations. Inset shows the memory kernel contribution K_C(t) from the reference simulation compared to the memory due to conservative interactions (ΔK^CG(t)) in CG GLE simulations parametrized with K̃(t).

Figure 2

Friction introduced by conservative interactions in NVT simulations using a Langevin thermostat, as a function of the applied friction coefficient. The data shown are based on simulations of the IBI model. An almost-perfect linear dependence is found, which is emphasized by the linear fit, shown as a black dotted line.

Figure 3

Results for iterative optimization of memory kernels for the IBI water model. (a, b, c) Comparison of the VACF for the IOMK method (panel (a)), the IMRV-1 method (panel (b)), and the IMRV-2 method (panel (c)). (d–f) Comparison of D(t) = ∫₀^t dsC_VV(s) for the IOMK method (panel (d)), the IMRV-1 method (panel (e)), and the IMRV-2 method (panel (f)).

Figure 4

Distinct VHF for (a) the AA reference, (b) the CG-MD IBI model, (c) the K̃-model, and (d) the IOMK model.

Figure 5

Distinct VHF at (a) R = 0.276 nm and (b) R = 0.2 nm, for different CG IBI models, compared to the AA reference.

Figure 6

VACFs from GLE simulations of CG models with a) two-body potentials b) three-body potentials, parametrized with K̃(t), compared to the AA reference.

Figure 7

Error estimate of the VACF based on eq 20, for all CG simulations.

Figure 8

VHF for the IOMK models with the IBI, the SW-FM and the SW-RE model, compared to the AA reference, for (a) R = 0.276 nm and (b) R = 0.2 nm.

Figure 9

Error estimate for the distinct VHF for all studied IBI, SW-FM, and SW-RE models.