This is a preprint.
Better than DFA? A Bayesian Method for Estimating the Hurst Exponent in Behavioral Sciences
- PMID: 36748008
- PMCID: PMC9900970
Better than DFA? A Bayesian Method for Estimating the Hurst Exponent in Behavioral Sciences
Abstract
Detrended Fluctuation Analysis (DFA) is the most popular fractal analytical technique used to evaluate the strength of long-range correlations in empirical time series in terms of the Hurst exponent, H. Specifically, DFA quantifies the linear regression slope in log-log coordinates representing the relationship between the time series' variability and the number of timescales over which this variability is computed. We compared the performance of two methods of fractal analysis-the current gold standard, DFA, and a Bayesian method that is not currently well-known in behavioral sciences: the Hurst-Kolmogorov (HK) method-in estimating the Hurst exponent of synthetic and empirical time series. Simulations demonstrate that the HK method consistently outperforms DFA in three important ways. The HK method: (i) accurately assesses long-range correlations when the measurement time series is short, (ii) shows minimal dispersion about the central tendency, and (iii) yields a point estimate that does not depend on the length of the measurement time series or its underlying Hurst exponent. Comparing the two methods using empirical time series from multiple settings further supports these findings. We conclude that applying DFA to synthetic time series and empirical time series during brief trials is unreliable and encourage the systematic application of the HK method to assess the Hurst exponent of empirical time series in behavioral sciences.
Keywords: detrended fluctuation analysis; fractal fluctuations; fractional; human movement; long-range correlation; physiology; variability.
Conflict of interest statement
Declarations. The authors declare no competing financial interests.
Figures




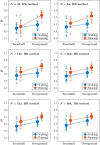


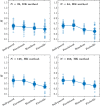






References
-
- Hurst H.E.: Long-term storage capacity of reservoirs. Transactions of the American Society of Civil Engineers 116(1), 770–799 (1951). 10.1061/TACEAT.0006518 - DOI
-
- Mandelbrot B.B., Wallis J.R.: Computer experiments with fractional Gaussian noises: Part 1, averages and variances. Water Resources Research 5(1), 228–241 (1969). 10.1029/WR005i001p00228 - DOI
-
- Beran J., Terrin N.: Estimation of the long-memory parameter, based on a multivariate central limit theorem. Journal of Time Series Analysis 15(3), 269–278 (1994). 10.1111/j.1467-9892.1994.tb00192.x - DOI
-
- Kantelhardt J.W., Berkovits R., Havlin S., Bunde A.: Are the phases in the Anderson model long-range correlated? Physica A: Statistical Mechanics and its Applications 266(1–4), 461–464 (1999). 10.1016/S0378-4371(98)00631-1 - DOI
-
- Efstathiou M., Varotsos C.: On the altitude dependence of the temperature scaling behaviour at the global troposphere. International Journal of Remote Sensing 31(2), 343–349 (2010). 10.1080/01431160902882702 - DOI
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
