Dissecting cell identity via network inference and in silico gene perturbation

Abstract

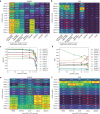
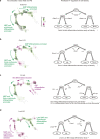
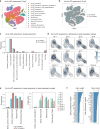
Cell identity is governed by the complex regulation of gene expression, represented as gene-regulatory networks¹. Here we use gene-regulatory networks inferred from single-cell multi-omics data to perform in silico transcription factor perturbations, simulating the consequent changes in cell identity using only unperturbed wild-type data. We apply this machine-learning-based approach, CellOracle, to well-established paradigms-mouse and human haematopoiesis, and zebrafish embryogenesis-and we correctly model reported changes in phenotype that occur as a result of transcription factor perturbation. Through systematic in silico transcription factor perturbation in the developing zebrafish, we simulate and experimentally validate a previously unreported phenotype that results from the loss of noto, an established notochord regulator. Furthermore, we identify an axial mesoderm regulator, lhx1a. Together, these results show that CellOracle can be used to analyse the regulation of cell identity by transcription factors, and can provide mechanistic insights into development and differentiation.

Fig. 1. Overview of CellOracle and application to haematopoiesis.

a, Simulation of cell-state transitions in response to TF perturbation. First, CellOracle constructs custom transcriptional GRNs using scRNA-seq and scATAC-seq data (left). Accessible promoter and enhancer peaks from scATAC-seq data are then combined with scRNA-seq data to generate cluster-specific GRN models (middle). CellOracle simulates the change in cell state in response to a TF perturbation, projecting the results onto the cell trajectory map (right). b, Force-directed graph of 2,730 myeloid progenitor cells from Paul et al.. Twenty-four cell clusters (Louvain clustering) were organized into six main cell types. Mk, megakaryocytes. c, Differentiation vectors for each cell projected onto the force-directed graph. d, CellOracle simulation of cell-state transition in Spi1 KO simulation. Summarized cell-state transition vectors projected onto the force-directed graph. Vectors for each cell are shown in the inset. e, Spi1 KO simulation vector field with perturbation scores (PSs). f, Gata1 KO simulation with perturbation scores. g, Schematic of Spi1–Gata1 lineage switching. MPP, multipotent progenitor. h, Detail of Gata1 simulation for the granulocyte branch. Left, cell-state transition vectors for each cell. Right, summarized vectors. i, Systematic KO simulation result of 90 TFs in the GM and ME lineage is summarized as a scatter plot of the sum of negative perturbation scores (shown in log scale). Dashed lines represent cut-off values corresponding to false-positive rate (FPR) = 0.01. Genes are classified into four categories on the basis of their previously reported functions (Supplementary Table 2). The asterisk refers to Supplementary Fig. 11, where we expand on the predicted phenotype. All scores can be explored through our web application (https://celloracle.org).

Fig. 2. Validation of CellOracle using experimentally measured cell density in Cebpa and Cebpe KOs in haematopoiesis.

a, Biological interpretation of perturbation scores (estimation of cell density based on perturbation score). Case 1: the differentiation and perturbation simulation vectors share the same direction, indicating a population shift towards a more differentiated identity. Case 2: the two vectors are opposed, suggesting that differentiation is inhibited. Case 3: predicted inhibition precedes promotion; thus, cells will be likely to accumulate. b,c, CellOracle Cebpa KO (b) and Cebpe KO (c) simulations showing cell-state transition vectors, perturbation scores and estimated cell density (Markov simulation). Right, schematics of simulated phenotype. Ery, erythrocyte. d, Ground-truth experimental cell density plot of wild-type (WT) cells, Cebpa KO cells and Cebpe KO cells in the force-directed graph embedding space. Estimated kernel density data are shown as a contour line on a scatter plot to depict cell density. e, Cell-type proportions in the WT and ground-truth KO samples. Gra, granulocyte; KDE, kernel density estimation; Mo, monocyte.

Fig. 3. CellOracle KO simulation with zebrafish embryogenesis data.

a, Two-dimensional force-directed graph of the axial mesoderm (AM) sub-branch (n = 1,669 cells) in a published zebrafish embryogenesis atlas (Farrell et al.). Arrows indicate notochord cell differentiation (top) and prechordal plate differentiation (bottom). b, Conversion of URD-calculated pseudotime (left) into a 2D pseudotime gradient vector field (right). c, Degree centrality scores were used to rank the top 30 TFs in notochord (left) and prechordal plate (right). Black text denotes TFs. Grey text denotes non-TFs. d, Expression of noto projected onto the axial mesoderm sub-branch. e, Noto KO simulation vector and perturbation scores. f, Markov simulation to estimate cell density in the noto KO sample. The simulation predicted inhibited early notochord differentiation and promotion of prechordal plate differentiation, indicating a potential lineage switch.

Fig. 4. Experimental validation of zebrafish noto LOF predictions.

a, UMAP plot of WT reference data for axial mesoderm (6, 8 and 10 hpf): notochord, early notochord, early axial mesoderm and prechordal plate clusters (n = 2,012 cells). Arrows indicate notochord differentiation (top) and prechordal plate differentiation (bottom). b, Gene expression (log-transformed unique molecular identifier (UMI) count) and developmental stage are projected onto the axial mesoderm UMAP plot. Noto and twist2 are expressed in notochord, whereas gsc marks the prechordal plate. c, Bar plots comparing cell cluster compositions between treatments and controls (left, flh^n1/n1 mutants (10 hpf) and controls; right, noto crispants (10 hpf) and tyr crispants). Cluster compositions are presented as the proportion of each group normalized to the whole cell number. In both flh^n1/n1 mutants and noto crispants, the notochord is significantly depleted (flh^n1/n1: P = 5.55 × 10⁻⁵²; noto: P = 1.39 × 10⁻³³, chi-square test) and the prechordal plate is significantly expanded (flh^n1/n1: P = 1.07 × 10⁻⁴; noto: P = 5.01 × 10⁻¹⁸, chi-square test. ***P < 0.001; ****P < 0.0001). d–g, flh^n1/n1 mutant or noto crispant data projected onto the WT axial mesoderm UMAP plot. d, Cluster annotation and sample label projected onto the UMAP plot. e, Kernel cell density contour plot shows control cell density (left) and flh^n1/n1 mutant cell density (right). f, Cluster annotation and sample label projected onto the UMAP plot. g, tyr crispant cell density (left) and noto crispant cell density (right) shown on the kernel cell density contour plot.

Fig. 5. Experimental validation of lhx1a as a putative regulator of zebrafish axial mesoderm development.

a, Top 30 TFs according to predicted KO effects. Red and *: previously reported notochord regulators (Supplementary Table 2). lhx1a, sebox and irx3a were selected for experimental validation. b, lhx1a LOF simulation in the axial mesoderm sub-branch, predicting an inhibition of axial mesoderm differentiation from early stages. c, scRNA-seq validation of experimental LOF: cell cluster composition of the axial mesoderm clusters normalized to the whole cell number in lhx1a and tyr (control) crispant samples. Early notochord is significantly expanded (P = 1.34 x 10⁻³⁵, chi-square test) and differentiated axial mesoderm populations are significantly depleted (notochord: P = 3.83 x 10⁻³; prechordal plate: P = 1.28 x 10⁻⁷, chi-square test) in lhx1a crispants. d, lhx1a and tyr crispant axial mesoderm cells at 10 hpf. Left, cell type annotation of lhx1 and tyr crispant cells. Right, lhx1a and control crispant data projected onto the WT UMAP. e, Control cell density (left, n = 2,342 cells) and lhx1a crispant cell density (right, n = 2,502 cells). f, Rug plot showing the difference in averaged NMF module scores between lhx1a and tyr crispants in notochord lineage cells. Black, cell-type-specific modules. Light grey, broad cluster modules. CM, cephalic mesoderm. g, Violin plot of NMF module score in notochord lineage cells (n = 1,918 lhx1a crispant and n = 2,616 tyr crispant cells. h, Violin plots of gene expression in the notochord (NC) lineage cells. ****P < 0.0001, two-tailed Wilcoxon rank-sum test with Bonferroni correction. i, Quantification (number of spots in flattened HCR image) normalized to WT. Mean ± s.e.m. n = 2 independent biological replicates, 8 embryos per replicate. nog1: P = 0.0022 (WT versus lhx1a crispant), P = 0.0052 (tyr versus lhx1a crispant); gsc: P = 0.00042 (WT versus lhx1a crispant), P = 0.0018 (tyr versus lhx1a crispant); twist2: P = 0.0011 (WT versus lhx1a crispant), P = 0.0012 (tyr versus lhx1a crispant); two-sided t-test. j, Representative HCR images for nog1 expression (yellow) in whole embryos at 10 hpf. k, Representative flattened HCR images of 10 hpf embryos stained with probes against gsc (yellow) and twist2 (red); nuclei are stained with DAPI (blue). Scale bars, 300 μm.

Extended Data Fig. 1. Overview of the CellOracle workflow.

(a) Overview of the CellOracle context-dependent GRN model construction method. First, genomic DNA sequence and TF-binding-motif information provide all potential regulatory links to construct a ‘base GRN.’ CellOracle uses scATAC-seq data to identify accessible promoter and enhancer DNA sequences in this step. The DNA sequence of these regulatory elements is scanned for TF-binding motifs, generating a list of potential regulatory connections between a TF and its target genes (left). Next, active connections (described below), dependent on cell state or cell type, are identified from all potential connections in the base GRN. CellOracle builds machine-learning (ML) models for this step that predict the quantitative relationship between the TF and the target gene. The ML model fitting results present the certainty of connection as a distribution, enabling the identification of GRN configurations by removing inactive connections from the base GRN structure. (b—d) Overview of signal propagation simulation. CellOracle leverages an inferred GRN model to simulate how target gene expression changes in response to the changes in regulatory gene expression. (b) The input TF perturbation (shown in yellow) is propagated side-by-side within the network model. (c) Input data and GRN coefficient matrix format used in the signal propagation calculation. (d) Leveraging the linear predictive ML algorithm features, CellOracle uses the GRN model as a function to perform the signal propagation calculation. Iterative matrix multiplication steps enable the estimation of indirect and global downstream effects resulting from the perturbation of a single TF. (e) After signal propagation, the simulated gene expression shift vector is converted into a 2D vector and projected onto the low-dimensional space. Details are described in the Methods.

Extended Data Fig. 2. Benchmarking of inferred GRN configurations.

(a,b) We benchmarked the CellOracle GRN modelling method against pre-existing GRN inference algorithms: WGCNA, DCOL, GENIE3, and SCENIC. Details of input data and ground-truth data are described in the Methods. We generated a base GRN using the Cusanovich mouse sci-ATAC-seq atlas dataset or UCSC mm9 promoter DNA sequence data. CellOracle scored better than or comparable to other algorithms. CellOracle results with a promoter base GRN received lower but comparable scores than the scATAC-seq base GRN results. In addition, we tested the CellOracle GRN method using two impaired base GRN datasets (Scrambled motif base GRN and no base GRN) to investigate how the base GRN data contributes to its performance. (a) AUROC (Area Under the Receiver Operating Characteristic curve) heat map. The top score in each condition is highlighted with a red rectangle. (b) EPR (Early Precision Ratio) heat map. EPR represents the EP ratio relative to the random model ER score. An EPR of less than 1 indicates that the GRN inference results are no better than random prediction. (c,d) The performance of CellOracle was tested after downsampling cells. GRN models were made after downsampling to 400, 200, 100, 50, 25, and 10 cells. We recommend at least 50 cells for GRN inference based on these results. CellOracle used the same mouse scATAC-seq base GRN as a and b. The Liver_2 sample contains less than 400 cells. (e,f) GRN inference performance comparison between different base GRN data generated from various tissue types. The top score in each condition is highlighted with a red rectangle.

Extended Data Fig. 3. CellOracle analysis of Paul et al. haematopoiesis data.

(a) Force-directed graph of 2,730 myeloid progenitor cells from Paul et al. with all clusters labelled. DC = Dendritic Cell; Ery = Erythrocyte; GMP = Granulocyte–Monocyte Progenitor; Gran = Granulocyte; Lym = Lymphoid; MEP = Megakaryocyte–Erythrocyte Progenitor; Mk = Megakaryocyte; Mo = Monocyte. We removed the DC and Lymphoid cell clusters to focus on myeloid cell differentiation. (b) Degree distribution of the MEP_0 cluster GRN model. After making the GRN model for each cluster, network edges were pruned. Then, we counted the network degree (k), representing the number of network edges for each gene. P(k) is the frequency of network degree k. The relationship between k and P(k) was visualized after log transformation to test whether the data follow a power law, in which there is a linear relationship between log(k) and log(P(k)). The R-squared value (R²) was calculated to quantify the degree of the linear relationship. The same analysis was performed on the randomized GRN (lower panel). (c) Top 30 genes ranked by degree centrality in the MEP_0 cluster GRN. (d) Gata1 gene expression (log-transformed UMI) projected onto the force-directed graph (left) and violin plot grouped by cell-type annotation (right). (e) Spi1 gene expression (log-transformed UMI) projected onto the force-directed graph (left) and violin plot grouped by cell-type annotation (right). (f) Systematic KO simulation of TFs in the GM (Granulocyte–Monocyte) and ME (Megakaryocyte–Erythrocyte) lineages. The sum of the negative perturbation scores is calculated for each TF to quantify the perturbation effect along each lineage. (g) Negative PS sum cut-off value calculation. Cut-off values were calculated for GM and ME lineage simulations based on the distribution of PS sum score calculated from the randomized simulation result (false-positive rate (FPR) = 0.01).

Extended Data Fig. 4. Perturbation score calculation and interpretation.

(a—d) Schematic for perturbation score (PS) calculation. CellOracle calculates a PS by comparing the direction of the simulated cell state transition with the direction of cell differentiation. (a) Schematic for differentiation vector calculations. First, the pseudotime data are summarized by grid points. Then, CellOracle calculates a 2D gradient vector of the pseudotime data representing the directionality of differentiation pseudotime. (b) Calculation of the inner-product value between the differentiation vector and gene perturbation vectors. First, the results of the perturbation simulation are converted into the same vector field format as the differentiation vector field, and the inner product of these vectors is calculated to produce a PS. (c) A positive PS (magenta) suggests the perturbation vector and differentiation vector share a similar direction, thus, suggesting the TF perturbation would promote differentiation. In contrast, a negative PS (green) represents inhibited differentiation. (d) Schematic for perturbation score interpretation. A positive perturbation score (green) predicts that the perturbation promotes differentiation. A negative perturbation score (purple) represents inhibited differentiation.

Extended Data Fig. 5. CellOracle TF KO simulation results for Paul et al. haematopoiesis data: part 1.

a–d, CellOracle KO simulation for four key TF regulators of haematopoiesis: Klf1 (a), Gfi1b (b), Gfi1 (c) and Irf8 (d) reported in^,. The simulated cell state transition vector field is visualized with perturbation scores (PS; magenta: negative score; green: positive score). The right column shows a summary of the TF role based on the CellOracle simulation results, cell transition vector, and PS. For example, a positive PS in the TF KO simulation (green) implies that the TF has a role in cell state maintenance or inhibiting cell differentiation. In contrast, a negative PS in the KO simulation (magenta) implies that the TF normally promotes cell differentiation.

Extended Data Fig. 6. CellOracle TF KO simulation results for Paul et al. haematopoiesis data: part 2.

a–d, CellOracle KO simulation results for Gata2 (a), Runx1 (b), Fli1 (c) and Lmo2 (d). The simulated cell state transition vector field is visualized with perturbation scores (PS; magenta: negative score; green: positive score). The right column shows a summary of the TF role based on the CellOracle simulation results, cell transition vector, and PS. For example, a positive PS in the TF KO simulation (green) implies that the TF has a role in cell state maintenance or inhibiting cell differentiation. In contrast, a negative PS in the KO simulation (magenta) implies that the TF normally promotes cell differentiation.

Extended Data Fig. 7. Dahlin et al. mouse haematopoiesis scRNA-seq data.

a, Force-directed graph of 44,082 myeloid progenitor cells from Dahlin et al. with all clusters labelled. MPP = Multipotent Progenitor; GMP = Granulocyte–Monocyte Progenitor; Gran = Granulocyte; LP = Lymphoid progenitor; MEP = Megakaryocyte–Erythrocyte Progenitor; Mk = Megakaryocyte; Mo = Monocyte; Baso = Basophil. (b) Marker gene expression (log-transformed UMI) projected onto the force-directed graph. Procr = MPP marker; Epor = Erythrocyte marker; Itga2b = Mk marker; Flt3 = LP marker; Mpo = Gran/Mo marker; Ms4a2 = Baso marker. (c) Pseudotime values projected onto the force-directed graph. (d) Differentiation vector calculated from the pseudotime gradient. ME and GM lineages are highlighted. (e) Csf1r and Cebpε gene expression projected onto the force-directed graph. The right panel is a magnified area of the GM lineage. Csf1r is a monocyte marker, and Cebpε is a granulocyte marker. (f) Early lineage bifurcation between monocytes and granulocytes is observed on the force-directed graph.

Extended Data Fig. 8. Setty et al. human haematopoiesis scRNA-seq data.

(a) Force-directed graph of 5,610 myeloid progenitor cells from Setty et al. with all clusters labelled. MPP = Multipotent Progenitor; GMP = Granulocyte–Monocyte Progenitor; Gran = Granulocyte; MEP = Megakaryocyte–Erythrocyte Progenitor; Mk = Megakaryocyte. (b) Marker gene expression (log-transformed UMI) projected onto the force-directed graph. PROCR = MPP marker; EPOR = Erythrocyte marker; ITGA2B = Mk marker; FLT3 = LP marker; MPO = Gran/Mo marker; MS4A2 = Baso marker. (c) Pseudotime values projected onto the force-directed graph. (d) Differentiation vector calculated from the pseudotime gradient. ME and GM lineages are highlighted. (e) CSF1R and CEBPE gene expression projected onto the force-directed graph. The right panel is a magnified area of the GM lineage. The CSF1R is a monocyte marker, and CEBPE is a granulocyte marker. (f) Early lineage bifurcation between monocytes and granulocytes is observed on the force-directed graph.

Extended Data Fig. 9. CellOracle validation using experimentally measured cell density in Tal1 KO in Pijuan-Sala et al. gastrulation and organogenesis scRNA-seq data.

(a) UMAP plot of chimeric E8.5 embryos of wild-type (WT) and Tal1 KO cells (25,307 cells and 26,311 cells, respectively) from a published scRNA-seq atlas of mouse gastrulation and organogenesis. (b) Tal1 gene expression (log-transformed UMI) projected onto the UMAP plot. (c) Pseudotime gradient vector field used in the perturbation score (PS) calculations. Developmental pseudotime was calculated using the DPT method with WT chimera scRNA-seq data and then converted into a 2D gradient vector field. (d) PS and cell transition vector field of the Tal1 KO simulation. (e) The magnified area of erythrocyte differentiation predicts inhibition or arrest of cell differentiation at the haematoendothelial progenitor stage. (f) The Markov random walk simulation result predicts high cell density in the haematoendothelial progenitor cluster and lower cell density at later stages, indicating that Tal1 KO would induce differentiation arrest at the haematoendothelial progenitor stage. (g) Experimentally measured Tal1 KO data. The kernel cell density of whole chimera (left), WT (middle), and Tal1 KO cells (right) were calculated after downsampling each condition (25,307 cells) to control for sample size. A scatter plot of whole chimera cells is shown as background (light grey) to highlight the overall cell trajectory structure. (h) The bar plot shows the cell type composition in each sample (right panel). Overall, the experimental result aligns with the simulated predictions. The relative fold change between WT and KO samples is also shown in Supplementary Table 4. (i) Perturbation score and cell transition vector field of the Tal1 conditional KO simulation in the erythroid lineage. Tal1 expression was set to zero in the Blood progenitor and Erythrocyte clusters; CellOracle simulates KO effects in later erythroid differentiation stages. (j) The Markov simulation result shows uniform cell density, predicting that Tal1 KO would not induce differentiation arrest in a conditional KO targeting later stages of erythroid differentiation.

Extended Data Fig. 10. CellOracle noto LOF simulation with Farrell et al. zebrafish embryogenesis data.

(a) 2D force-directed graph of a published atlas of zebrafish embryogenesis (n = 25,711 cells). (b) Main trajectory partitioned into four sub-branches. (c) Bar plots depicting the number of TFs after variable gene selection (black), the number of TFs with >1 network edge in the inferred GRN model (dark grey), and the number of TFs expressed in >1% of cells (light grey). (d) CellOracle noto LOF simulation result (left) and simulation results with a randomized GRN model (right) for the notochord lineage. Simulated cell state transitions for each cell were converted to a vector field and visualized with a scatter plot (shown in grey). (e) Noto LOF simulation for the prechordal plate lineage. (f) CellOracle noto LOF simulation vector is shown at single-cell resolution. Cells in the Notochord cluster are shown in orange, while the Prechordal Plate cells are shown in blue. The right panel is the magnified area. (g) Force-directed graph of the Other mesendoderm sub-branch with cell cluster annotations from the Farrell et al. study (n = 10,265 cells). (h) Pseudotime data are projected onto the force-directed graph. (i) The Somite lineage, defined in the previous Farrell et al. study, is in red. (j) Pseudotime gradient vector field calculated for the Somite lineage. (k) Noto LOF simulation vector field in the cells of the Somite lineage are shown with perturbation scores.

Extended Data Fig. 11. Zebrafish scRNA-seq experiments for noto LOF analysis.

(a) Schematic illustration of zebrafish scRNA-seq experiments. (1) The reference dataset was generated using cells from 6, 8, and 10 hpf wild-type (WT) embryos. To assess noto LOF, we also assayed (2) flh^n1/n1 mutants and (3) noto/flh crispants at 10 hpf (~25 embryos per sample; Methods). (b) Cell cluster composition comparing tyr crispant (control) with WT cells, showing similar cell distributions. After data integration, cell-type labels were transferred from the whole WT 6, 8, and 10 hpf reference data (see Methods). (c) Sample label projected onto the t-SNE plot. flh^n1/n1 mutant and control sample (left, n = 57,175 cells, 2 independent biological replicates for each sample), and t-SNE plot of noto crispant and tyr crispant samples (right, n = 9,185 cells, 2 biological, 3 technical replicates for noto crispant; n = 46,440 cells, n = 3 independent biological, 5 technical replicates for tyr crispant). (d) Cluster annotation label projected onto the t-SNE plot. WT zebrafish cells (left, n = 38,606 cells, two technical replicates per stage), flh^n1/n1 mutant and control sample (middle), noto crispant and tyr crispant samples (right). (e) Cell cluster composition comparing LOF samples with the control samples.

Extended Data Fig. 12. Zebrafish notochord regulator screening with CellOracle and initial experimental validation.

(a) Overview of the systematic LOF simulation and quantification method. CellOracle LOF simulation was performed for 232 TFs in the Notochord lineage to calculate the perturbation score (PS). The sum of the negative PS was calculated for each TF in the selected area between digitized pseudotime 0 to 3, before lineage specification. (b) Degree centrality score in the Notochord cluster GRN (left), gene expression specificity score in the Axial mesoderm sub-branch (middle), and mean expression value in the Axial mesoderm sub-branch (right) were calculated for the top 30 TFs selected in the systematic simulation to further prioritize candidate genes for experimental validation. We selected genes in the top 50% of these scores. Please refer to the Methods for the detailed selection procedure. We selected three candidates for experimental validation: lhx1a, sebox, and irx3a. (c,e,g) Cell cluster composition in axial mesoderm cells, comparing LOF (lhx1a, sebox, and irx3a) samples with control samples. Cell cluster composition comparison was performed with a Chi-square test, Two-tailed Bonferroni correction. lhx1a experiment: Early axial mesoderm p = 0.000229717, Early Notochord p = 1.08×10⁻²¹, Notochord p = 4.38×10⁻⁶, Prechordal Plate p = 1.42×10⁻¹⁰. Sebox experiment: Early axial mesoderm p = 3.01×10⁻⁶, Early Notochord p = 2.87×10⁻⁶, Notochord p = 4.38×10⁻⁶, Prechordal Plate p = 4.17×10⁻⁹. The left panels show cluster composition in the merged data, and the right panels show individual scRNA-seq batch. lhx1a LOF produced the most significant changes in cell composition. (d,f,h) Comparison of notochord marker gene expression between LOF and control samples. scRNA-seq gene expression in the Notochord lineage clusters is shown as a violin plot. Late-stage notochord markers, twist2 and nog1, or broad/early notochord markers, noto and tbxta, are visualized. Statistical tests: Wilcoxon rank-sum test, two-tailed with Bonferroni p-value correction. lhx1a experiment: twist2 p = 7.118×10⁻⁶⁴, nog1 p = 7.757×10⁻⁶⁷, noto p = 7.718×10⁻¹¹. sebox experiment: twist2 p = 8.022×10⁻¹⁰, nog1 p = 3.184×10⁻³, tbxta p = 1.551×10⁻³. irx3a experiment: twist2 p = 0.000012. (c) n = 720 cells and 1,686 cells for lhx1a crispant and tyr crispant, respectively. (e) n = 1,216 cells and 1,703 cells for sebox crispant and tyr crispant, respectively. (g) n = 1,176 cells and 1,651 cells for irx3a crispant and tyr crispant, respectively.

Extended Data Fig. 13. Zebrafish scRNA-seq experiments for lhx1a LOF analysis.

(a,b) t-SNE plot of lhx1a crispant (n = 45,582 cells, 4 biological replicates) and tyr control crispant samples (n = 76,163 cells, 5 biological, 7 technical replicates). (a) Cluster annotation labels transferred from WT reference data projected onto the t-SNE plot. (b) Sample label projected onto the t-SNE plot. (c) Cell cluster composition comparing lhx1a crispant and tyr control crispant samples as a proportion of cells from the whole embryo. (d) Cell density in the axial mesoderm is visualized as a kernel cell density contour plot. The cell number is downsampled to match the cell number before kernel cell density calculation (n = 260, 290, 336, and 367 for lhx1a crispant 1~4, n = 248, 234, 344, 316, 213, 286, and 350 for tyr crispant 1~7). The same contour threshold values are used for the visualization. (e) Cell cluster composition in the axial mesoderm clusters comparing lhx1a crispant and tyr control crispant samples. The left panels show cluster composition in the merged data, while the right panels show the individual scRNA-seq batch. (f) The top 30 NMF module weights for the Early notochord module (left) and the Late notochord module (right) are shown as a bar plot.