Fractal dimension complexity of gravitation fractals in central place theory

Abstract

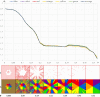
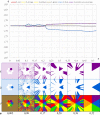
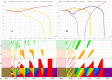
Settlement centers of various types, including cities, produce basins of attraction whose shape can be regular or complexly irregular (from the point of view of geometry). This complexity depends in part on properties of the space surrounding a settlement. This paper demonstrates that by introducing a dynamic approach to space and by including an equation of motion and space resistance, a dramatic change in the stylized static CPT (Central Place Theory) image occurs. As a result of the interplay of gravitational forces, basins of attraction arise around cities, whose boundaries appear to be fractals. This study provides a wealth of spatial fractal complex images which may change the traditional understanding of CPT.

Figure 1

Gravitational fractals in a CPT system. Legend: Points 1–6 represent six distinct cities (with six different colors) in a hexagonal force field; (A and D) represent illustrative fragments.

Figure 2

Methods of counting fractal dimensions for randomly selected magnifications of a fragment in hexagonal space. Legend: (A–C) Magnification of randomly selected fragment of fractal; (D) Boundary of attraction basins in selected fragment; (E) Ruler dimension determined by the 4 neighboring pixels of each boundary pixel; (F) Box dimension depends on 4 adjacent pixels with one of them being a boundary pixel.

Figure 3

Comparison of the variability of the global ruler and box dimensions. Legend: The edge of all attraction basins is a function of the μ coefficient; 1–edges of all basins, 2–entire basins.

Figure 4

The box dimension of the edges of the attraction basins depending on the μ coefficient (separately for each attractor). Legend: 1–boundaries of single attraction basins, 2–entire basins.

Figure 5

Box dimension of the attraction basins as a geometric irregular figure in the gravitational fractal. Legend: 1-basins of the first city, 2-basins of the second city, 7-basins of all cities.

Figure 6

Distribution of the values of fractal dimensions of the boundaries of the attraction basins identified in selected fragments of a fractal; Legend: (A, D)-fragments marked in Fig. 1.

Figure 7

Box dimension of the edge of each gravitation basin in A and D. Legend: The icons show the variability of the fragments A and D due to the share of the attraction basins of individual cities (3, 4 and 6).

Figure 8

Local dimensions of parts of the attraction basins treated as an irregular geometric figure in (A) and (D). Legend: The icons illustrate the variability of the shape of some of the attraction basins of individual cities in fragment (A) and (D) for cities 3, 4 and 6.