Learning high-order interactions for polygenic risk prediction

Abstract

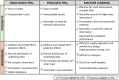
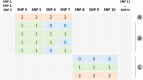
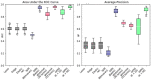
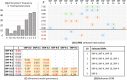
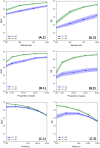
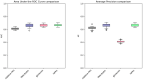
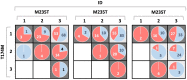
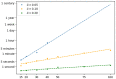
Within the framework of precision medicine, the stratification of individual genetic susceptibility based on inherited DNA variation has paramount relevance. However, one of the most relevant pitfalls of traditional Polygenic Risk Scores (PRS) approaches is their inability to model complex high-order non-linear SNP-SNP interactions and their effect on the phenotype (e.g. epistasis). Indeed, they incur in a computational challenge as the number of possible interactions grows exponentially with the number of SNPs considered, affecting the statistical reliability of the model parameters as well. In this work, we address this issue by proposing a novel PRS approach, called High-order Interactions-aware Polygenic Risk Score (hiPRS), that incorporates high-order interactions in modeling polygenic risk. The latter combines an interaction search routine based on frequent itemsets mining and a novel interaction selection algorithm based on Mutual Information, to construct a simple and interpretable weighted model of user-specified dimensionality that can predict a given binary phenotype. Compared to traditional PRSs methods, hiPRS does not rely on GWAS summary statistics nor any external information. Moreover, hiPRS differs from Machine Learning-based approaches that can include complex interactions in that it provides a readable and interpretable model and it is able to control overfitting, even on small samples. In the present work we demonstrate through a comprehensive simulation study the superior performance of hiPRS w.r.t. state of the art methods, both in terms of scoring performance and interpretability of the resulting model. We also test hiPRS against small sample size, class imbalance and the presence of noise, showcasing its robustness to extreme experimental settings. Finally, we apply hiPRS to a case study on real data from DACHS cohort, defining an interaction-aware scoring model to predict mortality of stage II-III Colon-Rectal Cancer patients treated with oxaliplatin.

Fig 1. Alternative approaches to polygenic risk scoring vs hiPRS.

Strengths (first row) and Weaknesses (second row) of three main categories of PRS methods discussed in the Introduction. The green tick signals that the given point of strength applies to hiPRS as well. The blue arrow signals a point of weaknesses that hiPRS algorithm does not suffer, or some aspect that the algorithm was specifically designed to solve.

Fig 2. hiPRS algorithm process flow.

(A) Input data is a list of genotype-level SNPs. (B) Focusing on the positive class only, the algorithm exploits FIM (apriori algorithm) to build a list of candidate interactions of any desired order, retaining those that have an empirical frequency above a given threshold δ. This leads to a filtered set of terms in the form of sequences of pairs of SNP and associated categorical level (i.e., allele frequency in this example). The sequences can include from a single SNP-allele pair up to a maximum number of pairs defined by the user (l_max). (C) The whole training data is then scanned, searching for these sequences and deriving a re-encoded dataset where interaction terms are binary features (i.e., 1 if sequence i is observed in j-th patient genotype, 0 otherwise). From this dataset we can compute the MI between each interaction and the outcome and (D) obtain a ranked list (I_δ) based on this metric. (E) Starting from the interaction at the top of I_δ, hiPRS constructs I_K, selecting K (where K is user-specified) terms through the greedy optimization of the ratio between MI (relevance) and a suitable measure of similarity for interactions (redundancy) (cf. Algorithm 1, Materials and methods). This leads to a set of predictive, yet diverse, interactions that (F) we use to define the score weighting their contribution by fitting a LR model and retaining the corresponding β coefficients.

Fig 3. Simulation data generating rules.

Graphical representation of the three rules that determine the positive class. Cases are obtained when A ∨ B ∨ C. More details on the generative model are provided in the Materials and Methods Section.

Fig 4. hiPRS results on risk prediction against benchmark PRSs and ML approaches.

AUC (left) and AP (right) performance distributions of 30 independent trials. In grey the three traditional penalized PRSs approaches with additive effects only; in violet the two ML algorithms (SVM-Behravan and DNN-Badre); in pink glinternet algorithm for two model dimensions (3 interactions, i.e. 36 terms, and 8 interactions, i.e. 93 terms); in green hiPRS for K = 10 and K = 40.

Fig 5. Interpretability analysis.

(A) Absolute frequency of the generative rules in the training data, limited to the positive class. (B) Interactions selected by hiPRS with K = 10 and corresponding β coefficients. (C) Coefficients of the glinternet model with 3 interaction terms: main effects are in gray, interactions in yellow. (D) Lists of SNPs selected by SVM-Behravan during its five internal cross validations, cf. Benchmark Algorithms in the Materials and Methods Section. Note: reported results are limited to one simulation among the 30 randomly generated datasets.

Fig 6. Sensitivity analysis results.

Average performance of hiPRS in terms of AUC and AP for variable sample size (A.1 and A.2), class imbalance (B.1 and B.2) and missing heritability, i.e. noise (C.1 and C.2). Confidence bands are at the 95% level. The x-axis is in logarithmic scale for panels C.1 and C.2.

Fig 7. Results and comparisons for a real biological setting.

AUC (left) and AP (right) performance distributions of 30 independent trials, sampled according to a real biological mechanism where SNPs regulate factors associated to atrial fibrillation. In grey, a traditional PRS with additive effects only; in violet the ML based algorithm, DNN-Badre; in pink glinternet (31 logistic terms); in green hiPRS (K = 13).

Fig 8. DACHS case study results.

Left panel: AUCs obtained by hiPRS and a benchmark model during cross-validation (four folds). Average AUCs are 0.72 and 0.57 respectively for hiPRS and the benchmark model. Right panel: interactions selected by hiPRS, and corresponding effect-sizes, when fitting the model on the whole dataset. In grey are reported the pathways each SNP belongs to (cf. Materials and methods).

Fig 9. Simulated atrial fibrillation data.

Schema of the distribution of cases (red section of the pie-plots) and controls (light blue section) in the case-control study described in [46], for each multilocus genotype combination of M235, T174M and ID. Dark gray cells are associated to higher risk of atrial fibrillation, while light gray cells are associated to protective combinations. The schema proposed here is based on the image reported in [45].

Fig 10. Time complexity of hiPRS.

Fitting times of hiPRS for different values of δ and different numbers of SNPs (x-axis). For better readability, the y-axis is reported in logarithmic scale. Dashed-lines are obtained via least-squares.