An electrically driven single-atom "flip-flop" qubit

Abstract

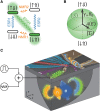
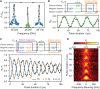
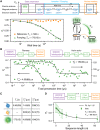
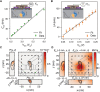
The spins of atoms and atom-like systems are among the most coherent objects in which to store quantum information. However, the need to address them using oscillating magnetic fields hinders their integration with quantum electronic devices. Here, we circumvent this hurdle by operating a single-atom "flip-flop" qubit in silicon, where quantum information is encoded in the electron-nuclear states of a phosphorus donor. The qubit is controlled using local electric fields at microwave frequencies, produced within a metal-oxide-semiconductor device. The electrical drive is mediated by the modulation of the electron-nuclear hyperfine coupling, a method that can be extended to many other atomic and molecular systems and to the hyperpolarization of nuclear spin ensembles. These results pave the way to the construction of solid-state quantum processors where dense arrays of atoms can be controlled using only local electric fields.

Fig. 1.. Flip-flop qubit and device layout.

(A) Energy level diagram of ³¹P donor electron (↑,↓) and nuclear (⇑,⇓) spin states, in the presence of a static magnetic field B₀ ∼ 1 T along the z direction. Electron spin resonance (ESR) and nuclear magnetic resonance (NMR) transitions are induced by oscillating magnetic fields. The flip-flop qubit is obtained by truncating the system to the ↓⇑ , ↑⇓ states, between which transitions are induced by EDSR. (B) Bloch sphere representation of the flip-flop qubit. (C) False-color scanning electron microscopy image of the device, comprising a single-electron transistor (SET) (cyan) to read out the electron spin, local gate electrodes (red and purple) to control the donor potential, and MW antennas (brown) for electric (left, open-circuit) and magnetic (right, short-circuit) control of the donor spins. Here and elsewhere, we use the color orange to represent properties related to the nuclear spin, blue for the electron spin, and green for the flip-flop qubit.

Fig. 2.. Coherent electrical drive.

(A) The frequency spectrum shows two ESR peaks separated by A = 114.1 MHz. The flip-flop resonance peak is at f_EDSR = 28.0966 GHz. (B) Coherent EDSR Rabi oscillation obtained by reading out the nuclear spin flip probability P_flip. A schematic of the pulse sequence is shown on top. (C) Reading out the electron and nuclear spin-up proportions simultaneously highlights the antiparallel flip-flop Rabi oscillations. A schematic of the pulse sequence is shown on top. (D) The Rabi chevron is mapped out by detuning the drive frequency around the resonance.

Fig. 3.. Relaxation, coherence, and gate fidelity.

(A) The flip-flop qubit relaxation time T_1ff = 173(12) s is measured by initializing the donor in the a∣↑⇓〉 + b∣↓⇓〉 state with ∣a∣² ≈ ∣b∣² ≈ 0.5 and replenishing the ∣↑⇓〉 state population with adiabatic aESR1 inversion pulses applied every 5 s to counteract the electron relaxation channel ∣↑⇓〉 → ∣↓⇓〉. (B) Fitting the Ramsey and the Hahn echo decays using an exponential decay reveals $T_{2\mathrm{ff}}^{\ast }=4.09(88)$ μs (with exponent 1.28) and $T_{2\mathrm{ff}}^{\mathrm{H}}=184(24)$ μs (exponent 2), respectively. (C) Tabulated values of the relaxation and coherence times measured on the electron, nuclear, and flip-flop qubits. (D) Randomized benchmarking (RB) experiment for the flip-flop qubit, yielding an average one-qubit gate fidelity ℱ_1Q = 98.4(2)%.

Fig. 4.. Electrical drive via hyperfine modulation.

(A) Linear dependence of the flip-flop Rabi frequencies on the voltage at the output of the MW source. (B) Stark shift of the hyperfine coupling produced by a dc voltage applied to the FD gate, as extracted from the shift of the NMR1 resonance frequency. An independent calibration of the line attenuation at MW confirms that the flip-flop qubit is driven by dynamic modulation of the hyperfine coupling. (C) Triangulation of the most probable location of the donor under study, obtained through COMSOL finite-element models informed by the capacitive coupling between the donor and each electrostatic gate (see section S5). The contours indicate the 1σ and 2σ confidence regions. (D) Amplitude of the MW electric field E_ac around the donor location, estimated using the same COMSOL model as above, assuming a voltage on the FD gate V_FD = 1 V_pp. We find E_ac ≈ 3.5 MV/m at the most likely donor location.

Fig. 5.. Experimental setup.

Wiring and instrumentation used to control and read out the donor spin qubit. The red dashed square defines the implantation region for this qubit device.

Fig. 6.. Electron spin-dependent tunneling.

(A) SET current as a function of two gate voltages. The pattern of Coulomb peaks (green) is broken (white dotted line) in the presence of a donor charge transition. The read position for the electron spin is indicated by a red dot and corresponds to the point where the donor electrochemical potential is equal to that of the SET island. (B and C) Schematic depiction of the electron spin-dependent tunneling between the donor and the SET island (left) with the corresponding SET current traces (right). The ³¹P donor is tunnel-coupled to the SET island with a potential barrier between them shown in cyan. The Fermi-Dirac distribution for the density of the occupied states at the SET is shown in green.

Fig. 7.. Nuclear spin initialization fidelity.

∣⇑〉 (A) ENDOR sequence containing consecutive aESR2 and aNMR1 pulses. The sequence starts and ends in the read phase to initialize the electron into the ∣↓〉 state. (B) Energy level diagrams for the ³¹P donor show nuclear spin initialization into the ∣⇑〉 state when we apply the ENDOR sequence in (A). With the electron initialized in the ∣↓〉 state in the read phase, we consider two cases of initial nuclear states before the ENDOR sequence: ∣⇓〉 (left diagram) and ∣⇑〉 (right diagram). (C) The histogram shows the final nuclear state after an ENDOR initialization sequence followed by nuclear spin readout with 25 shots. The nuclear spin is randomized after the 25 shots to test the ENDOR sequence again. We assign to ∣⇑〉 the instances where the probability P_↑ of finding the electron in the ∣↑〉 state is above 0.4. Samples where P_↑ < 0.4 threshold correspond to the nuclear spin ∣⇓〉 state, i.e., to the error of the ENDOR initialization. The histogram yields an ENDOR initialization fidelity of F = 90.88(55)%. The nuclear readout fidelity can be inferred by fitting the histogram peaks and calculating their overlap, yielding F_read > 99.99%.