Diffusion-Enhanced Förster Resonance Energy Transfer in Flexible Peptides: From the Haas-Steinberg Partial Differential Equation to a Closed Analytical Expression

Abstract

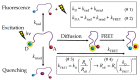
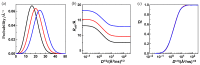
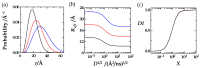
In the huge field of polymer structure and dynamics, including intrinsically disordered peptides, protein folding, and enzyme activity, many questions remain that cannot be answered by methodology based on artificial intelligence, X-ray, or NMR spectroscopy but maybe by fluorescence spectroscopy. The theory of Förster resonance energy transfer (FRET) describes how an optically excited fluorophore transfers its excitation energy through space to an acceptor moiety-with a rate that depends on the distance between donor and acceptor. When the donor and acceptor moiety are conjugated to different sites of a flexible peptide chain or any other linear polymer, the pair could in principle report on chain structure and dynamics, on the site-to-site distance distribution, and on the diffusion coefficient of mutual site-to-site motion of the peptide chain. However, the dependence of FRET on distance distribution and diffusion is not defined by a closed analytical expression but by a partial differential equation (PDE), by the Haas-Steinberg equation (HSE), which can only be solved by time-consuming numerical methods. As a second complication, time-resolved FRET measurements have thus far been deemed necessary. As a third complication, the evaluation requires a computationally demanding but indispensable global analysis of an extended experimental data set. These requirements have made the method accessible to only a few experts. Here, we show how the Haas-Steinberg equation leads to a closed analytical expression (CAE), the Haas-Steinberg-Jacob equation (HSJE), which relates a diffusion-diagnosing parameter, the effective donor-acceptor distance, to the augmented diffusion coefficient, J, composed of the diffusion coefficient, D, and the photophysical parameters that characterize the used FRET method. The effective donor-acceptor distance is easily retrieved either through time-resolved or steady-state fluorescence measurements. Any global fit can now be performed in seconds and minimizes the sum-of-square difference between the experimental values of the effective distance and the values obtained from the HSJE. In summary, the HSJE can give a decisive advantage in applying the speed and sensitivity of FRET spectroscopy to standing questions of polymer structure and dynamics.

Keywords: FRET; diffusion coefficient; distance distribution; fluorescence; peptide and polymer structure and dynamics.

Figure 1

DFRET: Diffusion-enhanced Förster resonance energy transfer. After excitation, the excited donor, D, can either become deactivated by emitting fluorescence (k_rad) or by being quenched, for instance, by iodine ions (k_nrad) or by transferring its excitation energy to the acceptor, A (k_FRET). FRET can take place at every D-A distance but is more likely to happen at shorter distances, which is why it is enhanced by D-A diffusion. The pertinent equations (I–IV) are explained in the main text.

Figure 2

(a) An exemplary probability distance distribution of the donor–acceptor distance in a linear (bio)polymer (b) The diffusion profile or R_eff (D^1/2) profile: Solving the HSE under variation of the diffusion coefficient results in values of the effective distance that range from L to R (dashed lines). The effective distance plotted against D^1/2 approaches R_eff = L when the extent of diffusional motion approaches zero and approaches R_eff = R when the extent of diffusional motion approaches infinity. (c) The diffusion-influence profile or DI(D^1/2) profile is obtained when the diffusion profile shown in (b) is normalized with L and R according to DI = (R_eff − L)/(R − L) (Equation (11)). The diffusion influence, DI, can adapt values between 0 (0%) and 1 (100%). (d) The diffusion-influence profile, the DI(J^1/2) or DI(X) profile: The diffusion influence plotted against the square root of the augmented diffusion coefficient, X = J^1/2 (see Equation (12)).

Figure 3

(a) Three different 3-D Gaussian distance distributions (black, red, blue). (b) The corresponding diffusion profiles (black, red, blue) with the effective distance plotted against the square root of the diffusion coefficient. The donor lifetime, the Förster radius, and the left integration limit were kept constant (τ_D = 100 ns, R₀ = 10 Å, r_L = 2.5 Å) (c) After normalization (Equation (11)), the three profiles became identical.

Figure 4

(a) A 3-D Gaussian distance distribution (b) Four diffusion profiles obtained with (a) four different donor lifetime constants, τ_D, of 100 ns (red), of 30 ns (blue), of 10 ns (green), and of 1 ns (black). The Förster radius (R₀ = 15 Å) and the left integration limit (r_L = 3 Å) were held constant. (c) Diffusion-influence profiles after normalization. (d) The DI-profiles coincide when the DI values are plotted against the square root of the product of diffusion coefficient and donor lifetime.

Figure 5

(a) Three ideal-chain distance distributions (Equation (18)) with b = 18 Å, r_L = 3 Å (black curve); b = 24 Å, r_L = 4 Å (red curve); and b = 30 Å, r_L = 5 Å (blue curve). (b) The corresponding diffusion profiles obtained with b = 18 Å, r_L = 3 Å, R₀ = 9 Å (black curve); with b = 24 Å, r_L = 4 Å, R₀ = 12 Å (red curve); and with b = 30 Å, r_L = 5 Å, R₀ = 15 Å (blue curve). Thus, for all three evaluated distributions (black, red, blue), the ratio R₀/r_L equaled 3. (c) The corresponding diffusion-influence profiles with DI plotted against X (X = J^1/2). The three profiles merge into one.

Figure 6

The HSE was solved for two different series of ideal-chain distributions (Equation (18)). R₀ was varied from 9 Å to 15 Å, and r_L was varied from 1.5 Å to 5 Å. The donor lifetime was held constant (τ_D = 100 ns). In one series of distributions, the constant b was chosen as b = 1.5⋅R₀ ranging from 13.5 Å to 22.5 Å, in the other series as b = 2⋅R₀ ranging from 18 Å to 30 Å. (a) Exemplary distributions for the two series with r_L = 3 Å, R₀ = 10 Å and either b = 1.5⋅R₀ = 15 Å (blue curve) or b = 2⋅R₀ = 20 Å (black curve). (b) The DI(X) profiles overlap for both distributions shown in (a). (c) All DI(X) profiles were analyzed by using Equation (13).

Figure 7

The results for X₀ and M (solid circles in panels (a,b) obtained for the range of R₀ = 9–15 Å, r_L = 1.5–5 Å with b = 2R₀, and R₀/r_L > 3) were fitted to second-degree polynomial functions (solid lines in panels (a,b) given in Table 2).

Figure 8

The Haas-Steinberg–Jacob equation (HSJE) is a closed analytical equation decomposed here into simple equations, I to VIII, for clarity. With the coefficients shown here (a₀ to b₃), it is valid for R₀ 9–15 Å and r_L 1.5–5 Å.