Operational analysis for COVID-19 testing: Determining the risk from asymptomatic infections

Abstract

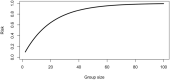
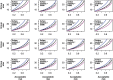
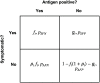
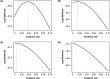
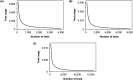
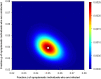
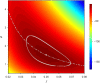
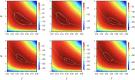
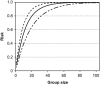
Testing remains a key tool for managing health care and making health policy during the coronavirus pandemic, and it will probably be important in future pandemics. Because of false negative and false positive tests, the observed fraction of positive tests-the surface positivity-is generally different from the fraction of infected individuals (the incidence rate of the disease). In this paper a previous method for translating surface positivity to a point estimate for incidence rate, then to an appropriate range of values for the incidence rate consistent with the model and data (the test range), and finally to the risk (the probability of including one infected individual) associated with groups of different sizes is illustrated. The method is then extended to include asymptomatic infections. To do so, the process of testing is modeled using both analysis and Monte Carlo simulation. Doing so shows that it is possible to determine point estimates for the fraction of infected and symptomatic individuals, the fraction of uninfected and symptomatic individuals, and the ratio of infected asymptomatic individuals to infected symptomatic individuals. Inclusion of symptom status generalizes the test range from an interval to a region in the plane determined by the incidence rate and the ratio of asymptomatic to symptomatic infections; likelihood methods can be used to determine the contour of the rest region. Points on this contour can be used to compute the risk (defined as the probability of including one asymptomatic infected individual) in groups of different sizes. These results have operational implications that include: positivity rate is not incidence rate; symptom status at testing can provide valuable information about asymptomatic infections; collecting information on time since putative virus exposure at testing is valuable for determining point estimates and test ranges; risk is a graded (rather than binary) function of group size; and because the information provided by testing becomes more accurate with more tests but at a decreasing rate, it is possible to over-test fixed spatial regions. The paper concludes with limitations of the method and directions for future work.

Fig 1. The risk of groups of different sizes (Eq 3) when the true fraction of infected individuals is f_t = 0.05 (i.e., we set f^=0.05 in Eq 3).

This figure can be used to determine the risk associated with groups of different sizes (ranging from 2 to 100) by choosing a group size on the x-axis, drawing a vertical line to intersect the curve, drawing a horizontal line that intersects the y-axis, and reading off the level of risk.

Fig 2. Sixteen realizations of the group size as a function of acceptable risk using the simulation methods described in [30].

In all panels, the number of tests is T = 2500, the true incidence rate is f_t = 0.05, and the probabilities of false negative and false positives tests are 0.25 and 0.05. The dotted line shows the group size consistent with the level of acceptable risk when the incidence rate is f_t, the solid black line is the group size using the estimate in Eq 1 determined using the positivity rate from the individual realization of the simulation, and the red and blue lines are the group sizes using the maximum and minimum estimates for incidence rate, $f_{upper}=\widehat{f}+0.5·Range(\widehat{f}$) and $f_{lower}=\widehat{f}-0.5·Range\left(\widehat{f}\right)$, respectively. One key observation is that the group size determined if the incidence rate were known (dotted line) falls between those determined from the upper and lower limits of incidence rate determined by the test range.

Fig 3. The population divided into four classes according to infection and symptom status.

A fraction f_t of the population is symptomatic and infected (antigen positive); such individuals have a probability of a false negative test p_SFN. A fraction g_t of the population is symptomatic but not infected; such individuals have a probability of a false positive test p_SFP. A fraction ρ_tf_t of the population is infected but not symptomatic; such individuals have a probability of a false negative test p_AFN. Finally, fraction 1 − f_t − g_t − ρ_tf_t = 1 − f_t(1 + ρ_t) − g_t of the population is neither infected nor symptomatic; such individuals have a probability of a false positive test p_AFP. The subscript t indicates that these three parameters characterize the true state of the world, however none of them are observable.

Fig 4. Behavior of the log-likelihood function.

Shown is the log-likelihood function (the logarithm of the right side of Eq 6) as the positivity rate declines when p_FN = 0.25, p_FP = 0.05 and T = 100 tests are administered for positivity (A) 0.075, (B) 0.06, (C) 0.0525, and (D) 0.04.

Fig 5. The normalized likelihoods for incidence rate.

Shown are normalized likelihoods (i.e., posteriors with a uniform prior) when p_FN = 0.25, p_FP = 0.05, and positivity is (A) 0.025, (B) 0.0125, or (C) 0.00625. The colored curves correspond to different numbers of tests shown in the legend inset; since positivity is specified, higher numbers of tests are associated with lower levels of positivity.

Fig 6. The test range for incidence rate.

Shown are the test ranges for posteriors with a uniform prior when p_FN = 0.25, p_FP = 0.05, and positivity is (A) 0.025, (B) 0.0125, or (C) 0.00625.

Fig 7. Results of simulating the process of testing.

Shown (for ease of presentation) are the first 100 values of the point estimates for f_t (upper left panel), g_t (upper right panel), and ρ_t (lower left panel). The lower right panel is an expanded version of the point estimates for ρ_t. Each circle represents the value of ${\widehat{f}}_n,{\widehat{g}}_n$, or ${\widehat{\rho }}_n$ on the n^th replicate of the simulation. The thick red lines represent the averages over the entire 1000 simulations. There are also black lines at the true values of the three parameters. In the lower right panel, the y-axis is expanded to show that the mean of the ${\widehat{\rho }}_n$ exceeds ρ_t; see the text for an explanation. The means of ${\widehat{f}}_n$ and ${\widehat{g}}_n$ essentially sit on top of the true values; again see the text for an explanation. The thin dotted lines show the means of the estimates ±1.96 times their standard deviations.

Fig 8. The likelihood (Eq 37) of the fractions of individuals who are infected and symptomatic, f, and uninfected and symptomatic g, when the test data are the means of T_S and P_S.

The white dot denotes the true values of the parameters.

Fig 9. The profile log-likelihood (Eq 40) for the fraction of individuals who are infected and symptomatic f and the ratio of of the fraction of individuals who are infected and asymptomatic to those who are infected and symptomatic ρ when the test data are the means of T_S, P_S, and P.

The white dot denotes the true values of the parameters. The 95% CR contour is shown in white for the exact binomial likelihoods and in gray for the Gaussian approximation to those likelihoods. The white dotted line is obtained by replacing $\widehat{g}$ in Eq 28 by its MLE value, replacing $\widehat{f}$ by an arbitrary value f, and then viewing the right side as an equation for the ratio ρ(f) of asymptomatic to symptomatic infected individuals.

Fig 10. The consequences of varying test numbers and letting test data vary from the mean values of T_S, P_S and P.

In each panel the white dot represents f_t and ρ_t, and the dotted curve is the function ρ(f) described in the caption to the previous figure and which now depends on the test results. The upper left panel reproduces Fig 9, in which T = 1500 and the test data are the mean values of T_S, P_S, and P. In the other panels, the test data are a random realization of the simulation of the testing process and going clockwise from the upper left panel, T = 2000, 3000, 3500, 4000, and 4500.

Fig 11. The risk of including asymptomatic individuals in groups of different sizes.

The solid line corresponds to using the MLEs for $\widehat{f},\widehat{g}$, and $\widehat{\rho }$ in the risk formula (Eq 44), and the two dotted lines correspond to using the minimum and maximum values of ρf on the 95% CR contour.