Twin-field quantum key distribution without optical frequency dissemination

Abstract

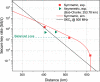
Twin-field (TF) quantum key distribution (QKD) has rapidly risen as the most viable solution to long-distance secure fibre communication thanks to its fundamentally repeater-like rate-loss scaling. However, its implementation complexity, if not successfully addressed, could impede or even prevent its advance into real-world. To satisfy its requirement for twin-field coherence, all present setups adopted essentially a gigantic, resource-inefficient interferometer structure that lacks scalability that mature QKD systems provide with simplex quantum links. Here we introduce a technique that can stabilise an open channel without using a closed interferometer and has general applicability to phase-sensitive quantum communications. Using locally generated frequency combs to establish mutual coherence, we develop a simple and versatile TF-QKD setup that does not need service fibre and can operate over links of 100 km asymmetry. We confirm the setup's repeater-like behaviour and obtain a finite-size rate of 0.32 bit/s at a distance of 615.6 km.

Fig. 1. Schematics of TF-QKD setups.

In TF-QKD, the users (Alice and Bob) communicate with each other by sending encoded quantum signals at the single-photon level to the intermediate node (Charlie), who measures the interference using two single photon detectors. The protocolʼs stringent requirement for phase stability has rendered all existing setups to adopt a closed interferometer configuration, which is resource-inefficient and inflexible. a Existing Mach–Zehnder interferometer setup^,,. Alice and Bob inherit a common optical frequency ν_R that is disseminated by Charlie via the long service fibres. b Open channel setup. Alice and Bob locally generate their own optical frequencies and their coherent side-bands of ν_A ± f₀ and ν_B ± f₀, with a nominally identical microwave frequency offset f₀. One side-band is used to reconcile the laser frequency difference (Δν = ν_A − ν_B), while the other is allocated quantum signal encoding. The open scheme eliminates the need for the service fibre and the optical frequency locking hardware, and supports asymmetric links.

Fig. 2. Experimental setup.

Alice (Bob) owns an independent ultrastable laser, the signal of which is modulated by a phase modulator (PM) to produce a frequency comb of 25 GHz spacing. Two comb lines separated by 100 GHz are chosen for quantum signal encoding (λ_q) and channel stabilisation (λ_c), respectively. Charlie contains a receiving 50/50 beam splitter to interfere the incoming signals. The λ_q photons are registered by D₀ and D₁ and the λ_c photons by D_c. D_cʼs count rate is used as error signal to the fast PID controller that cancels the twin-field phase fluctuation of the λ_c signals. a Optical frequency comb measured after the PM; b Encoder box. DWDM dense wavelength-division multiplexing; EPC electrically driven polarisation controller; FS fibre stretcher; IM intensity modulator; VOA variable optical attenuator.

Fig. 3. Open quantum channel stabilisation.

Alice and Bobʼs lasers are fully independent, and their frequency difference is adjustable by offsetting Aliceʼs laser to a high-fineness cavity. Except a, all data in this figure were measured with the 615.6 km quantum fibre. a Histograms of phase compensation signals integrated over 10 ms time intervals for a 10 m quantum link; b same as a but with 615.6 km quantum link; c compensation signal angular frequency as a function of the laser frequency offset (Δν). Error bars represent standard deviation. The blue line is a guide to the eye and has a slope of 1. d Optical output power as a function of time measured at one output of Charlieʼs 50/50 interfering beam-splitter; Purple (green): channel reference or the λ_c signal when the FPGA PID controller is turned off (on); Orange: slowed drift of the λ_q signal. e–g The phase angle distributions of the channel reference before (purple) and after (green) the simplex channel stabilisation, measured for laser frequency offsets of −2, 0 and 2 kHz, respectively. Symbol σ represents standard deviation. Data in panels d–g were measured with a power metre.

Fig. 4. Secure key rate (SKR) simulations and results.

The AOPP-SNS TF-QKD with finite size effects was implemented in the experiments. Two sets of experimental data are included. Symmetric case (squares): The usersʼ losses to Charlie are strictly matched while their fibre lengths may differ by 10 km; Asymmetric case (triangles): Bobʼs fibre length is fixed at 253.78 km. The green dashed line indicates the expected SKR when the asymmetry to Bobʼs 253.78 km fibre is treated by just adding attenuation. A fibre attenuation coefficient of 0.168 dB km⁻¹ is adopted for calculating the SKR simulation (red line) and the absolute repeaterless SKC₀ bound (black line) for an ideal point-point QKD setup operating at 500 MHz.