Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Jul 1;50(3):675-690.
doi: 10.1080/02664763.2021.1947996. eCollection 2023.

Classification of histogram-valued data with support histogram machines

Ilsuk Kang  1 , Cheolwoo Park  2 , Young Joo Yoon  3 , Changyi Park  4 , Soon-Sun Kwon  5 , Hosik Choi  6
Affiliations

Classification of histogram-valued data with support histogram machines

Ilsuk Kang et al. J Appl Stat. .

Abstract

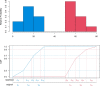
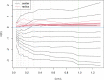
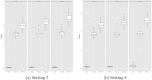
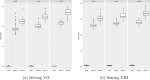
The current large amounts of data and advanced technologies have produced new types of complex data, such as histogram-valued data. The paper focuses on classification problems when predictors are observed as or aggregated into histograms. Because conventional classification methods take vectors as input, a natural approach converts histograms into vector-valued data using summary values, such as the mean or median. However, this approach forgoes the distributional information available in histograms. To address this issue, we propose a margin-based classifier called support histogram machine (SHM) for histogram-valued data. We adopt the support vector machine framework and the Wasserstein-Kantorovich metric to measure distances between histograms. The proposed optimization problem is solved by a dual approach. We then test the proposed SHM via simulated and real examples and demonstrate its superior performance to summary-value-based methods.

Keywords: 62H30; Support vector machines; Wasserstein-Kantorovich metric; symbolic data.

PubMed Disclaimer

Conflict of interest statement

No potential conflict of interest was reported by the author(s).

Figures

Figure 1.
Figure 1.
The top panel displays two observed histograms and the bottom shows the corresponding empirical cumulative distribution. The bottom plot illustrates how to obtain the redefined subintervals and the common relative frequency from two histograms.
Figure 2.
Figure 2.
A solution path for SHM. The data are generated from Setting 1 in Section 3.1. The x axis represents 1/λ and the y axis the solutions. The black and red solid lines are the solutions for the center and the radius, respectively. The green vertical line indicates the optimal λ chosen by 10-fold cross-validation.
Figure 3.
Figure 3.
(Binary class cases) Misclassification errors with 100 replications for Settings 1–6. Three methods are compared: SHM, SVM with sample means, and k-NN with sample means. (a) Setting 1. (b) Setting 2. (c) Setting 3. (d) Setting 4. (e) Setting 5 and (f) Setting 6.
Figure 4.
Figure 4.
(Binary class cases) Misclassification errors with 100 replications for Settings 7 and 8. The total number of variables for classification is p = 20, 50, and 100. (a) Setting 7 and (b) Setting 8.
Figure 5.
Figure 5.
(Multi-class cases) Misclassification errors with 100 replications for Settings I–VI. Three methods are compared: SHM, SVM with sample means, and k-NN with sample means to classify three classes. (a) Setting I. (b) Setting II. (c) Setting III. (d) Setting IV. (e) Setting V and (f) Setting VI.
Figure 6.
Figure 6.
(Multi-class cases) Misclassification errors with 100 replications for Settings VII and VIII. The total number of variables for classification is p = 20, 50, and 100. (a) Setting VII and (b) Setting VIII.
Figure 7.
Figure 7.
Example of (a) Pullover and (b) Sandal label. (c)–(f) display the selected histograms from two different labels.
See this image and copyright information in PMC

References

    1. Alaei A. and Roy P.P., A new method for writer identification based on histogram symbolic representation, 14th International Conference on Frontiers in Handwriting Recognition, Heraklion, 2014, pp. 216–221.
    1. Angulo C., Anguita D., Abril L.G., and Ortega J.A., Support Vector Machines for Interval Discriminant Analysis, Neurocomput. 71 (2008), pp. 1220–1229.
    1. Billard L. and Diday E., From the statistics of data to the statistics of knowledge: Symbolic data analysis, J. Am. Stat. Assoc. 98 (2003), pp. 470–487.
    1. Billard L. and Diday E., Symbolic Data Analysis: Conceptual Statistics and Data Mining, Wiley, Chichester, 2007.
    1. Bottou L., Cortes C., Denker J.S., Druncker H., Guyon I., Jackel L., LeCun Y., Muller U.A., Sackinger E., Simard P., and Vapnik V., Comparison of classifier methods: a case study in handwritten digit recognition, Proceedings of the 12th IAPR International Conference on Pattern Recognition, Vol. 3 – Conference C: Signal Processing (Cat. No.94CH3440–5), 1994, pp. 77–82 vol.2. 10.1109/ICPR.1994.576879. - DOI

LinkOut - more resources