Hypotheses on a tree: new error rates and testing strategies
- PMID: 36825068
- PMCID: PMC9945647
- DOI: 10.1093/biomet/asaa086
Hypotheses on a tree: new error rates and testing strategies
Abstract
We introduce a multiple testing procedure that controls global error rates at multiple levels of resolution. Conceptually, we frame this problem as the selection of hypotheses that are organized hierarchically in a tree structure. We describe a fast algorithm and prove that it controls relevant error rates given certain assumptions on the dependence between the p-values. Through simulations, we demonstrate that the proposed procedure provides the desired guarantees under a range of dependency structures and that it has the potential to gain power over alternative methods. Finally, we apply the method to studies on the genetic regulation of gene expression across multiple tissues and on the relation between the gut microbiome and colorectal cancer.
Keywords: False discovery rate; Hierarchical testing; Multiple testing; Selective inference.
Figures
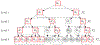



References
-
- Benjamini Y & Bogomolov M (2014). Selective inference on multiple families of hypotheses. J. R. Statist. Soc. B 76, 297–318.
-
- Benjamini Y & Heller R (2007). False discovery rates for spatial signals. J. Am. Statist. Assoc 102, 1272–81.
-
- Benjamini Y & Hochberg Y (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Statist. Soc. B 57, 289–300.
-
- Benjamini Y & Yekutieli D (2001). The control of the false discovery rate in multiple testing under dependency. Ann. Statist 29, 1165–88.

