Optimization of parameters in coherent spin dynamics of radical pairs in quantum biology

Abstract

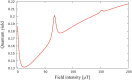
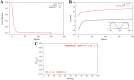
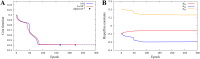
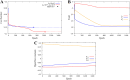
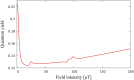
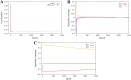
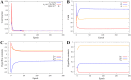
Identification of the external electromagnetic fields and internal hyperfine parameters which optimize the quantum singlet-triplet yield of simplified radical pairs modeled by Schrödinger system with spin Hamiltonians given by the sum of Zeeman interaction and hyperfine coupling interaction terms are analyzed. A method that combines sensitivity analysis with Tikhonov regularization is implemented. Numerical results demonstrate that the quantum singlet-triplet yield of the radical pair system can be significantly reduced if optimization is pursued simultaneously for both external magnetic fields and internal hyperfine parameters. The results may contribute towards understanding the structure-function relationship of a putative magnetoreceptor to manipulate and enhance quantum coherences at room temperature and leveraging biofidelic function to inspire novel quantum devices.

Fig 1. Dependence of the singlet yield on the strength of the applied magnetic field.

Singlet yield is minimized for low level magnetic fields. Hyperfine constants are chosen as A_1x = −0.234, A_1y = −0.234, A_1z = 0.117 all in mT. These values are chosen in the spirit of [25].

Fig 2. One proton model field optimization.

Identification of magnetic parameters for a one-proton model with hyperfine constants A_1x = −0.234, A_1y = −0.234, and A_1z = 0.117. Epoch stands for iteration parameter n. A: Minimization of the cost function. B: Magnetic parameter evolution. C: Final value of the cost function versus distance of initial iteration from the optimal parameter.

Fig 3. One proton model hyperfine optimization.

Identification of hyperfine paramters for a one-proton model. The cost function minimum $\mathcal{J}=0.14$ is reached for diagonal hyperfine constants A_1x = −0.054, A_1y = −0.198 and A_1z = 0.131 and using a regularization parameter λ = 10⁻⁵. A: Cost function minimization with or without regularization. B: Hyperfine parameter evolution.

Fig 4. Identification of the magnetic field and hyperfine parameters for a one-proton model.

Identification of the magnetic field and hyperfine parameters for a one-proton model. The cost function minimum $\mathcal{J}=0.106$ is reached for hyperfine constants A_1x = −0.089, A_1y = −0.053, A_1z = 0.155 for a magnetic field (u_x, u_y, u_z) = (-4.92, -19.33, -18.81) μT. A: Cost function minimization with or without regularization. B: Magnetic field parameter evolution. C: Hyperfine parameter evolution.

Fig 5. Quantum yield as a function of magnetic field for two-proton model.

Hyperfine constants are chosen as A_1x = 0.03, A_1y = −0.64, A_1z = 0.17, A_2x = −0.10, A_2y = 0.0, A_2z = 0.05 all in mT.

Fig 6. Identification of magnetic parameters for a two-proton model.

Iterative method decreases quantum yield to its minimum value $\mathcal{J}=0.13$ represented by the dose-response model. This minimum corresponds to fields (u_x, u_y, u_z) = (2.4, −17.3, −1.7) μT. Negative u_z indicates opposite direction as coordinate frame. Field azimuthal symmetry is lost for this model. A: Cost function minimization for different values of the regularization parameter. B: Magnetic field parameter evolution.

Fig 7. Identification of magnetic parameters for a two-proton model.

Iterative method decreases the quantum yield to its minimum value represented by the dose-response model. Optimal values of the hyperfine parameters are A_1x = 0, A_1y = 0, A_1z = −0.004, A_2x = −0.2, A_2y = 0, A_2z = 0.52. A: Cost function minimization with regularization. B: First proton hyperfine parameter evolution. C: Second proton hyperfine parameter evolution.

Fig 8. Identification of hyperfine and field parameters for a two-proton model.

Quantum yield decreases significantly compared to static response model and reaches the minimum $\mathcal{J}=0.11$ for hyperfine parameters A_1x = 0.081, A_1y = −0.186, A_1z = 0.104, A_2x = −0.232, A_2y = 0.119, A_2z = 0.848 and field (u_x, u_y, u_z) = (−12.9, −3.7, −8.1) μT. A: Cost function minimization with and without regularization. B: Field parameter evolution. C: First proton hyperfine parameter evolution.D: Second proton hyperfine parameter evolution.