Biologically-Based Computation: How Neural Details and Dynamics Are Suited for Implementing a Variety of Algorithms
- PMID: 36831788
- PMCID: PMC9954128
- DOI: 10.3390/brainsci13020245
Biologically-Based Computation: How Neural Details and Dynamics Are Suited for Implementing a Variety of Algorithms
Abstract
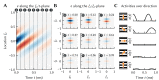
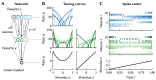
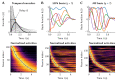
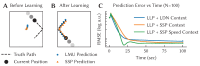
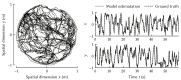
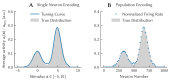
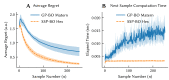
The Neural Engineering Framework (Eliasmith & Anderson, 2003) is a long-standing method for implementing high-level algorithms constrained by low-level neurobiological details. In recent years, this method has been expanded to incorporate more biological details and applied to new tasks. This paper brings together these ongoing research strands, presenting them in a common framework. We expand on the NEF's core principles of (a) specifying the desired tuning curves of neurons in different parts of the model, (b) defining the computational relationships between the values represented by the neurons in different parts of the model, and (c) finding the synaptic connection weights that will cause those computations and tuning curves. In particular, we show how to extend this to include complex spatiotemporal tuning curves, and then apply this approach to produce functional computational models of grid cells, time cells, path integration, sparse representations, probabilistic representations, and symbolic representations in the brain.
Keywords: cognitive modelling; neural engineering framework; spatial semantic pointers; spatiotemporal representation; time cells.
Conflict of interest statement
T.C.S. and C.E. have a financial interest in Applied Brain Research, Incorporated, holder of the patents related to the material in this paper (patent 17/895,910 is additionally co-held with the National Research Council Canada). The company or this cooperation did not affect the authenticity and objectivity of the experimental results of this work. The funders had no role in the direction of this research; in the analyses or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Figures








References
-
- Eliasmith C., Anderson C.H. Neural Engineering: Computation, Representation, and Dynamics in Neurobiological Systems. MIT Press; Cambridge, MA, USA: 2003.
-
- Choo X. Ph.D. Thesis. University of Waterloo; Waterloo, ON, Canada: 2018. Spaun 2.0: Extending the World’s Largest Functional Brain Model.
-
- Reed S., Zolna K., Parisotto E., Colmenarejo S.G., Novikov A., Barth-Maron G., Gimenez M., Sulsky Y., Kay J., Springenberg J.T., et al. A generalist agent. arXiv. 20222205.06175
Grants and funding
LinkOut - more resources
Full Text Sources

