A System-Independent Derivation of Preferential Attachment from the Principle of Least Effort

Abstract

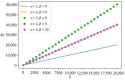
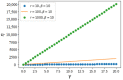
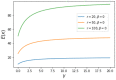
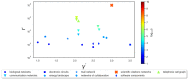
Preferential attachment (PA) is a widely observed behavior in many living systems and has been used in modeling many networks. The aim of this work is to show that the mechanism of PA is a consequence of the fundamental principle of least effort. We derive PA directly from this principle in maximizing an efficiency function. This approach not only allows a better understanding of the different PA mechanisms already reported but also naturally extends these mechanisms with a non-power law probability of attachment. The possibility of using the efficiency function as a general measure of attachment efficiency is also investigated.

Keywords: calculus of variation; least effort; maximum efficiency; power law; preferential attachment.

Figure 1

Variation of efficiency $\eta$ of attachment as a function of r for different fixed values of $\beta$ and $\gamma$. We notice that $\eta$ increases almost linearly with increasing r and depends little on $\beta$.

Figure 2

Variation of efficiency $\eta$ of attachment as a function of $\gamma$ with fixed $\beta =10$ and several values of $r$. We notice that $\eta$ increases almost linearly with increasing $\gamma$ in this interval of variation.

Figure 3

Variation of the average of x as a function of $\gamma$ with several values of $\beta$ and $r$.

Figure 4

Illustration of certain values of efficiency η (vertical axis right) calculated from empirical values of $r$ found in [20] for different networks. We chose γ = 1 because all these networks are described with the degree distribution $p\left(x\right)\propto x^{{\gamma }^{\prime }}$. The exponent ${\gamma }^{\prime }$ is represented on the abscissa. The color of the symbols changes from blue to red with increasing value of $\eta$.