Water Dynamics in Highly Concentrated Protein Systems-Insight from Nuclear Magnetic Resonance Relaxometry

Abstract

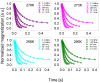
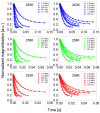
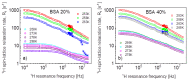
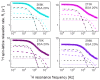
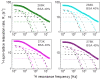
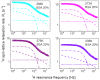
¹H spin-lattice relaxation experiments have been performed for water-Bovine Serum Albumin (BSA) mixtures, including 20%wt and 40%wt of BSA. The experiments have been carried out in a frequency range encompassing three orders of magnitude, from 10 kHz to 10 MHz, versus temperature. The relaxation data have been thoroughly analyzed in terms of several relaxation models with the purpose of revealing the mechanisms of water motion. For this purpose, four relaxation models have been used: the data have been decomposed into relaxation contributions expressed in terms of Lorentzian spectral densities, then three-dimensional translation diffusion has been assumed, next two-dimensional surface diffusion has been considered, and eventually, a model of surface diffusion mediated by acts of adsorption to the surface has been employed. In this way, it has been demonstrated that the last concept is the most plausible. Parameters describing the dynamics in a quantitative manner have been determined and discussed.

Keywords: dynamics; proteins; relaxation.

Figure A1

Normalized ¹H magnetization curves for BSA–water mixture (20%wt BSA) at selected resonance frequencies in the temperature range from 298 K to 268 K. Solid lines—single exponential fits.

Figure A2

Normalized ¹H magnetization curves for BSA–water mixture (40%wt BSA) at selected resonance frequencies in the temperature range from 278 K to 266 K. Solid lines—single exponential fits.

Figure A3

Normalized ¹H magnetization curves for BSA–water mixture (20%wt BSA) at selected resonance frequencies in the temperature range from 263 K to 253 K. Solid lines—single exponential fits. On the left frequencies are selected from the entire range measured and, on the right, only from areas with quadrupole peaks.

Figure A4

Normalized ¹H magnetization curves for BSA–water mixture (40%wt BSA) at selected resonance frequencies in the temperature range from 263 K to 253 K. Solid lines—single exponential fits. The frequencies are selected from the entire range measured.

Figure 1

¹H spin-lattice relaxation rates for BSA–water mixtures versus temperature, (a) 20%wt of BSA, (b) 40%wt of BSA. Stars show the changes in the relaxation rates upon cooling down.

Figure 2

(a) Ratio between spin-lattice relaxation rates for BSA–water mixtures (40%wt of BSA and 20%wt of BSA); (b) rescaled spin-lattice relaxation data for BSA–water mixtures compared with data for solid BSA.

Figure 3

¹H spin-lattice relaxation data for BSA–water mixture (20%wt of BSA) reproduced in terms of Equation (3); black solid line—overall fit decomposed into a contribution associated with intermediate dynamics (dashed-dotted black line) and fast dynamics (dashed black line), there is no relaxation contribution associated with slow dynamics. Comparison fits obtained in terms of Equation (5) are shown as the corresponding color lines (the lines are hardly visible as they almost overlap with the black ones), they are decomposed into Lorentzian term (dashed-dotted line), a term associated with three-dimensional translation diffusion (dashed line) and frequency independent term (dotted line).

Figure 4

¹H spin-lattice relaxation data for BSA–water mixture (40%wt of BSA) reproduced in terms of Equation (3); black solid line—overall fit decomposed into a contribution associated with slow dynamics (dashed-dotted black line), intermediate dynamics (dashed grey line), and fast dynamics (dashed black line). Comparison fits obtained in terms of Equation (5) are shown as the corresponding color lines, they are decomposed into a Lorentzian term (dashed-dotted line), a term associated with three-dimensional translation diffusion (dashed line) and a frequency independent term (dotted line).

Figure 5

¹H spin-lattice relaxation data for BSA–water mixture (20%wt of BSA) reproduced in terms of Equation (8); solid line—overall fit decomposed into a Lorentzian term (dashed-dotted line), a term associated with two-dimensional translation diffusion (dashed line) and a frequency independent term (dotted line).

Figure 6

¹H spin-lattice relaxation data for BSA–water mixture (40%wt of BSA) reproduced in terms of Equation (9); solid line—overall fit decomposed into a Lorentzian term (dashed-dotted line), a term associated with two-dimensional translation diffusion (dashed line) and a frequency independent term (dotted line).

Figure 7

¹H spin-lattice relaxation data for BSA–water mixture (20%wt of BSA) reproduced in terms of Equation (8); solid line—overall fit decomposed into a term associated with two-dimensional translation diffusion (dashed line), a Lorentzian term (dashed-dotted line) and a frequency independent term (dotted line).

Figure 8

¹H spin-lattice relaxation data for BSA–water mixture (40%wt of BSA) reproduced in terms of Equation (8); solid line—overall fit decomposed into a term associated with two-dimensional translation diffusion (dashed line), a Lorentzian term (dashed-dotted line) and a frequency independent term (dotted line).

Figure 9

¹H spin-lattice relaxation data for BSA–water mixture (40%wt of BSA) at 263 K reproduced as a sum of Equation (3) (¹H-¹H relaxation contribution) and Equation (10) (¹H-¹⁴N relaxation contribution); solid line—overall fit decomposed into the ¹H-¹H relaxation contributions associated with slow, intermediate, and fast dynamics (dashed lines), dashed-dotted line—¹H-¹⁴N relaxation contribution, dotted line—a frequency independent term.

Figure 10

Comparison of correlation times obtained by means of different models.