Practical Understanding of Cancer Model Identifiability in Clinical Applications

Abstract

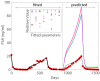
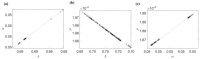
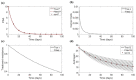
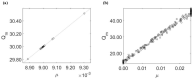
Mathematical models are a core component in the foundation of cancer theory and have been developed as clinical tools in precision medicine. Modeling studies for clinical applications often assume an individual's characteristics can be represented as parameters in a model and are used to explain, predict, and optimize treatment outcomes. However, this approach relies on the identifiability of the underlying mathematical models. In this study, we build on the framework of an observing-system simulation experiment to study the identifiability of several models of cancer growth, focusing on the prognostic parameters of each model. Our results demonstrate that the frequency of data collection, the types of data, such as cancer proxy, and the accuracy of measurements all play crucial roles in determining the identifiability of the model. We also found that highly accurate data can allow for reasonably accurate estimates of some parameters, which may be the key to achieving model identifiability in practice. As more complex models required more data for identification, our results support the idea of using models with a clear mechanism that tracks disease progression in clinical settings. For such a model, the subset of model parameters associated with disease progression naturally minimizes the required data for model identifiability.

Keywords: clinical application; computational oncology; mathematical model; mathematical oncology; model identifiability; observing-system simulation experiment; precision treatment; prostate cancer.

Figure 1

Figure adapted from Wu et al. [24] with permission distributed under a Creative Commons Attribution (CC BY) license. The color of the fitted parameters corresponds to the forecast trajectory of the same color. In the fitting portion, five different sets of parameters produce nearly indistinguishable good fits to the data. However, in the forecasting portion, only one set provides accurate forecasting.

Figure 2

An example of data fitting with only PSA synthetic data. In this example, the parameters being fitted are $\lambda$ and $\rho$ with ${\sigma }_0=0$. (a) Fitting of PSA. (b) Simulation of the S using the best fitted parameters. (c) Simulation of D using the best fitted parameters.

Figure 3

Parameter relation obtained from the 2-combination parameter test for the case of ${\sigma }_0=0$. (a) $\alpha$ and $\lambda$ are positively correlated. (b) $\rho$ and $\lambda$ are negatively correlated. (c) $\alpha$ and $\rho$ are positively correlated. If the parameters are linearly correlated, (a,b) would imply that $\alpha$ and $\rho$ are negatively correlated; however, this is not the case in (c). This suggests all three parameters are involved in a non-linear relationship.

Figure 4

An example of data fitting with PSA and androgen synthetic data. In this example, the parameters being fitted are $\mu$ and $Q_m$ with ${\sigma }_0=0$. (a) Fitting of PSA. (b) Simulation of the cancer population using the best fitted parameters. (c) Simulation of the parameter $\nu$ (associated with treatment resistance) using the best fitted parameters. (d) Fitting of androgen.

Figure 5

Parameter relation obtained from the 2-combination parameter test. (a) When ${\sigma }_0=0$, $\mu$ and $Q_m$ are slightly correlated with the best fit values concentrated around $\mu =9.00\times {10}^{-3}$ and $Q_m=30$. (b) When ${\sigma }_0=5\%$, the relationship between $\mu$ and $Q_m$ is much clearer, leading to a larger ARE%.