Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Feb 13;16(4):1572.
doi: 10.3390/ma16041572.

An Extended Hydro-Mechanical Coupling Model Based on Smoothed Particle Hydrodynamics for Simulating Crack Propagation in Rocks under Hydraulic and Compressive Loads

Dianrui Mu  1 , Aiping Tang  1 , Haigang Qu  1 , Junjie Wang  2
Affiliations

An Extended Hydro-Mechanical Coupling Model Based on Smoothed Particle Hydrodynamics for Simulating Crack Propagation in Rocks under Hydraulic and Compressive Loads

Dianrui Mu et al. Materials (Basel). .

Abstract

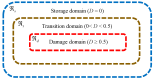
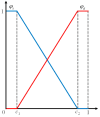
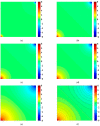
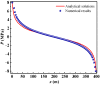
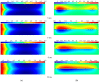
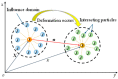
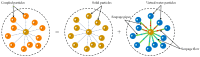
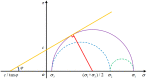
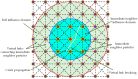
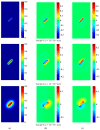
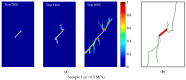
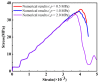
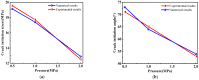
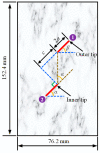
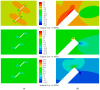
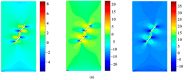
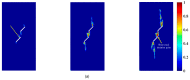
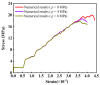
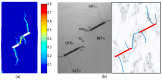
A seepage model based on smoothed particle hydrodynamics (SPH) was developed for the seepage simulation of pore water in porous rock mass media. Then, the effectiveness of the seepage model was proved by a two-dimensional seepage benchmark example. Under the framework of SPH based on the total Lagrangian formula, an extended hydro-mechanical coupling model (EHM-TLF-SPH) was proposed to simulate the crack propagation and coalescence process of rock samples with prefabricated flaws under hydraulic and compressive loads. In the SPH program, the Lagrangian kernel was used to approximate the equations of motion of particles. Then, the influence of flaw water pressure on crack propagation and coalescence models of rock samples with single or two parallel prefabricated flaws was studied by two numerical examples. The simulation results agreed well with the test results, verifying the validity and accuracy of the EHM-TLF-SPH model. The results showed that with the increase in flaw water pressure, the crack initiation angle and stress of the wing crack decreased gradually. The crack initiation location of the wing crack moved to the prefabricated flaw tip, while the crack initiation location of the shear crack was far away from the prefabricated flaw tip. In addition, the influence of the permeability coefficient and flaw water pressure on the osmotic pressure was also investigated, which revealed the fracturing mechanism of hydraulic cracking engineering.

Keywords: crack propagation; hydro-mechanical coupling; osmotic pressure; seepage model; smoothed particle hydrodynamics (SPH).

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
The interacting particles transfer water flow through virtual links.
Figure 2
Figure 2
Seepage domain of porous rock mass media [35,36].
Figure 3
Figure 3
Linear interpolation function of the seepage model [35,36].
Figure 4
Figure 4
Two-dimensional seepage model for an intact rock sample. (a) Schematic diagram of the five-point well network, reprinted from Ref. [38]. (b) Geometric model.
Figure 5
Figure 5
Cloud map of water pressure distribution for the intact sample at different seepage times (unit: MPa). (a) t = 0.1 d. (b) t = 1 d. (c) t = 2 d. (d) t = 3 d. (e) t = 100 d. (f) Analytical solution [38].
Figure 6
Figure 6
Numerical and analytical solutions for the water pressure of particles located on the diagonal line of y = x.
Figure 7
Figure 7
A two-dimensional seepage model for a rock sample with a prefabricated horizontal penetrating flaw. (a) Geometric model. (b) Numerical model.
Figure 8
Figure 8
Seepage process of a sample with a prefabricated horizontal penetrating flaw at different times. (a) Pore water pressure. (b) Vertical seepage velocity.
Figure 9
Figure 9
Deformation diagram of particle i under external force load, adapted from Ref. [25].
Figure 10
Figure 10
Dual characterization of coupled particles i under osmotic pressure.
Figure 11
Figure 11
Mohr–Coulomb failure criterion, reprinted from Ref. [48].
Figure 12
Figure 12
Virtual link fracture and crack propagation in the immediate neighborhood, adapted from Refs. [50,51].
Figure 13
Figure 13
The program calculation flow chart of the EHM-TLF-SPH model considering osmotic pressure.
Figure 14
Figure 14
Geometric model of a rock sample with a single prefabricated flaw.
Figure 15
Figure 15
The pore water pressure and osmotic pressure of samples with a prefabricated flaw under different permeability coefficients (p = 0.5 MPa). (a) Pore water pressure. (b) Horizontal osmotic pressure. (c) Vertical osmotic pressure.
Figure 16
Figure 16
The seepage velocity and osmotic pressure distribution of rock samples with a prefabricated flaw under different flaw water pressures (κ = 1.0 × 10−8 m/s). (a) Horizontal seepage velocity (unit: ×10−4 m/s). (b) Vertical seepage velocity (unit: ×10−4 m/s). (c) Horizontal osmotic pressure (unit: MPa). (d) Vertical osmotic pressure (unit: MPa).
Figure 17
Figure 17
Crack initiation and propagation of rock samples with a prefabricated flaw under uniaxial compression and different flaw water pressures. (a,c,e) Numerical results. (b,d,f) Experimental result, reprinted from Ref. [52].
Figure 17
Figure 17
Crack initiation and propagation of rock samples with a prefabricated flaw under uniaxial compression and different flaw water pressures. (a,c,e) Numerical results. (b,d,f) Experimental result, reprinted from Ref. [52].
Figure 18
Figure 18
Stress−strain curves of rock samples with a prefabricated flaw under uniaxial compression and different flaw water pressures.
Figure 19
Figure 19
Crack initiation stress and crack initiation angle of rock samples with a prefabricated flaw under uniaxial compression and different flaw water pressures. (a) Crack initiation stress. (b) Crack initiation angle.
Figure 20
Figure 20
Geometric model of the sample with two parallel prefabricated flaws.
Figure 21
Figure 21
Maximum principal stress at monitoring points of rock samples under uniaxial compression and different flaw water pressures.
Figure 22
Figure 22
Maximum principal stress distribution of rock samples with two parallel prefabricated flaws under uniaxial compression and different flaw water pressures (ABAQUS results). (a) Maximum principal stress. (b) Detailed view of the inner tip of the prefabricated flaw 2.
Figure 23
Figure 23
Maximum principal stress distribution of rock samples with two parallel prefabricated flaws under uniaxial compression and different flaw water pressures (EHM-TLF-SPH results). (a) Maximum principal stress. (b) Detailed view of the inner tip of the prefabricated flaw 2.
Figure 23
Figure 23
Maximum principal stress distribution of rock samples with two parallel prefabricated flaws under uniaxial compression and different flaw water pressures (EHM-TLF-SPH results). (a) Maximum principal stress. (b) Detailed view of the inner tip of the prefabricated flaw 2.
Figure 24
Figure 24
Crack propagation and coalescence modes of the sample with two parallel prefabricated flaws under uniaxial compression and different flaw water pressures (α = 45°, β = 45°). (a) Sample 1 (p = 0 MPa). (b) Sample 2 (p = 4 MPa). (c) Sample 3 (p = 8 MPa).
Figure 24
Figure 24
Crack propagation and coalescence modes of the sample with two parallel prefabricated flaws under uniaxial compression and different flaw water pressures (α = 45°, β = 45°). (a) Sample 1 (p = 0 MPa). (b) Sample 2 (p = 4 MPa). (c) Sample 3 (p = 8 MPa).
Figure 25
Figure 25
Stress–strain curves of rock samples with two parallel prefabricated flaws with different water pressures under uniaxial compression load.
Figure 26
Figure 26
Crack propagation and coalescence modes of the sample with two parallel prefabricated flaws under uniaxial compression and 0.5 MPa flaw water pressure (α = 30°, β = 45°). (a) Horizontal seepage velocity (unit: mm/s). (b) Horizontal seepage velocity (unit: mm/s). (c) Crack propagation and coalescence.
Figure 27
Figure 27
Crack propagation and coalescence of the sample containing two parallel prefabricated flaws with an inclination angle of 30° under uniaxial compression (α = 30°, β = 30°, and p = 0.5 MPa). (a) GPD results, reprinted from Ref. [4]. (b) Experimental results, reprinted from Ref. [55].
See this image and copyright information in PMC

References

    1. Liu Q.S., Gan L., Wu Z.J., Zhou Y. Analysis of spatial distribution of cracks caused by hydraulic fracturing based on zero-thickness cohesive elements. J. China Coal Soc. 2018;43:393–402. (In Chinese)
    1. Silva B.G., Einstein H.H. Finite Element study of fracture initiation in flaws subject to internal fluid pressure and vertical stress. Int. J. Solids Struct. 2014;51:4122–4136. doi: 10.1016/j.ijsolstr.2014.08.006. - DOI
    1. Robert Y.J. Ph.D. Thesis. University of Texas; Austin, TX, USA: 2018. Advanced Hydraulic Fracture Modeling: Peridynamics, Inelasticity, and Coupling to FEM.
    1. Bi J., Zhou X.P. A novel numerical algorithm for simulation of initiation, propagation and coalescence of flaws subject to internal fluid pressure and vertical stress in the framework of general particle dynamics. Rock Mech. Rock Eng. 2017;50:1833–1849. doi: 10.1007/s00603-017-1204-4. - DOI
    1. Zheng F., Zhuang X.Y., Zheng H., Jiao Y.-Y., Rabczuk T. Discontinuous deformation analysis with distributed bond for the modelling of rock deformation and failure. Comput. Geotech. 2021;139:104413. doi: 10.1016/j.compgeo.2021.104413. - DOI

LinkOut - more resources