3D DEM Simulations and Experiments on Spherical Impactor Penetrating into the Elongated Particles

Abstract

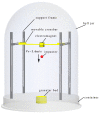
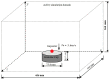
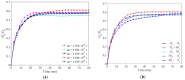
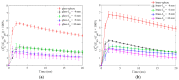
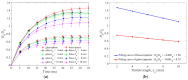
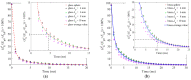
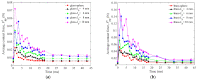
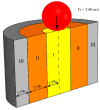
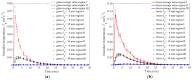
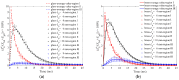
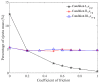
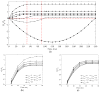
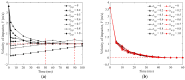
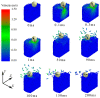
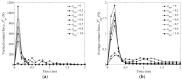
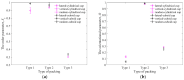
In this study, a brass or glass spherical impactor vertically penetrating into a granular bed composed of mono-sized spherical or elongated particles was simulated with three-dimensional (3D) discrete element method (DEM). Good agreement of the particle masses in the cup before and after penetration can be found in the simulations and experiments. The effects of particle length (L_p), friction coefficient, and particle configuration on the penetration depth of the impactor, ejecta mass, and solid volume fraction describing the response of the granular bed are discussed. The penetration depth is negatively correlated with L_p as the corresponding solid volume fraction of the granular bed decreases. A smaller friction coefficient leads to a larger penetration depth of the impactor and more ejection of particles. When the impactor is penetrating the L_p = 10 mm elongated particles, the penetration depth is negatively correlated to the order parameter and solid volume fraction.

Keywords: discrete element method; elongated particles; impact experiment; impaction; particle orientation.

Figure 1

Schematic drawing of the experimental apparatus. (The arrow represents the velocity direction of the impactor.)

Figure 2

Schematic diagram of numerical setup. (The arrow represents the velocity direction of the impactor.)

Figure 3

(a) Comparison of the penetration depth of glass impactor for five different time steps in DEM simulations. (b) Comparison of the penetration depth of glass impactor for five different cups in DEM simulations. (The length of elongated particles is 10 mm, the velocity of glass impactor is 3.60 m/s, and D_c and H_c are shown in Table 2).

Figure 4

(a) Influence of particle length on ejecta masses for both glass and brass impactors in DEM simulations. (b) Comparison of ejecta mass as a function of particle length between experiments and simulations. (The length of 2 mm represents the data of 2 mm spheres here and all the simulation parameters are from Table 2).

Figure 5

Kinetic energy $E_{\mathrm{k}}^{\mathrm{e}}$ of ejected particles as a function of time for granular bed of spherical particles and elongated particles of four particle lengths in DEM simulations: (a) is for the glass impactor, and (b) is for the brass impactor.

Figure 6

(a) H₀/D₀ versus time for granular bed of spheres and elongated particles of four lengths. (b) The fitting curves of the H₀/D₀ and particle length L_p for glass and brass impactors. H₀ and D₀ represent the penetration depth and diameter of the impactor, respectively.

Figure 7

Kinetic energy of impactor $E_{\mathrm{k}}^{\mathrm{i}}$ as a function of time for granular bed of spherical particles and elongated particles of four lengths: (a) is for the glass impactor, and (b) is for the brass impactor.

Figure 8

Average contact force of particles $F_{\mathrm{pp}}^{\mathrm{c}}$ as a function of time for 2 mm sphere and L_p = 4 mm, 6 mm, 8 mm, 10 mm elongated particles for DEM simulations: (a) is for the glass impactor, and (b) is for the brass impactor.

Figure 9

Diagram of sub-region division for granular bed. Region I: 0 < R₁ < 2/7R_c; region II: 2/7R_c < R₂ < 5/7R_c; and region III: 5/7R_c < R₃ < R_c. (The particles count in one region if their mass centers fall in this region; R_c is the radius of the cup).

Figure 10

(a) Comparison of solid volume fraction ϕ_p as a function of particle length L_p between experiments and simulations for both glass and brass impactors. (b) Initial solid volume fraction ϕ_p of the whole granular bed or three regions of granular bed as a function of particle length L_p before impact. The particle length of 2 mm represents the data of 2 mm spheres here.

Figure 11

Granular temperature T_p of particles in three regions versus time for granular bed with L_p = 4 mm, 6 mm, 8 mm, 10 mm elongated particles: (a) is for the glass impactor, and (b) is for the brass impactor.

Figure 12

Kinetic energy of particles in the cup $E_{\mathrm{k}}^{\mathrm{c}}$ in three regions versus time for granular bed with L_p = 4 mm, 6 mm, 8 mm, 10 mm elongated particles: (a) is for the glass impactor, and (b) is for the brass impactor.

Figure 13

Relationship between percentage of ejecta mass and friction coefficient μ_p-p, μ_i-p, and μ_w-p for L_p = 6 mm elongated particles. Condition I: μ_i-p = 0.2, μ_w-p = 0.34 and various μ_p-ps; condition II: μ_p-p = 0.2, μ_w-p = 0.34 and various μ_i-ps; condition III: μ_p-p = 0.2, μ_i-p = 0.2 and various μ_w-ps.

Figure 14

Time evolution of the non-dimensional penetration depth H₀/D₀ of impacting into the granular bed of L_p = 6 mm particles: (a) condition I, (b) condition II, and (c) condition III. H₀ and D₀ represent the penetration depth and diameter of impactor, respectively. Condition I: μ_i-p = 0.2, μ_w-p = 0.34 and various μ_p-ps; condition II: μ_p-p = 0.2, μ_w-p = 0.34 and various μ_i-ps; condition III: μ_p-p = 0.2, μ_i-p = 0.2 and various μ_w-ps. (The dotted lines are used to clearly mark the position of the impactor at different times.)

Figure 15

Time evolution of vertical velocity of impactor with sphere impacting into the granular bed of L_p = 6 mm elongated particles: (a) condition I and (b) condition II and III. Condition I: μ_i-p = 0.2, μ_w-p = 0.34 and various μ_p-ps; condition II: μ_p-p = 0.2, μ_w-p = 0.34 and various μ_i-ps; condition III: μ_p-p = 0.2, μ_i-p = 0.2 and various μ_w-ps. (The dotted lines are used to clearly mark the velocity of the impactor at different times).

Figure 16

Velocity profiles of elongated particles (L_p = 6 mm) impacted by brass impactor. (L_p = 6 mm, μ_p-p = 0.8, arrow represents velocity of impactor, whose color remains unchanged.)

Figure 17

(a) $F_{\mathrm{ip}}^{\mathrm{c}}$ as a function of time, $F_{\mathrm{ip}}^{\mathrm{c}}$ is the vertical contact force between impactor and particles; and (b) $F_{\mathrm{pp}}^{\mathrm{c}}$ as a function of time, $F_{\mathrm{pp}}^{\mathrm{c}}$ is the average contact force between all particles.

Figure 18

Diagram of regular configuration of elongated particles (L_p = 10 mm): (a,b) are lateral arrangement and vertical arrangement in the cylindrical cup; (c,d) are the lateral arrangement and vertical arrangement in the cuboid cup.

Figure 19

Comparison between solid volume fractions for different packing types (type 1—lateral arrangement, type 2—vertical arrangement, and type 3—random arrangement). The length of particles in the cup is 10 mm.

Figure 20

The order parameters and orientational parameters of three packings in cylindrical cup and cuboid cup: (a) is the order parameters for three packing types; (b) is the orientational parameters for three packing types (type 1—lateral arrangement, type 2—vertical arrangement, and type 3—random arrangement). The length of particles in the cup is L_p = 10 mm.

Figure 21

Comparison between ejecta masses for three packing types in cylindrical cup and cuboid cup. The length of particles in the cup is AR = 5.

Figure 22

Comparison between H₀/D₀ for three packing types in cylindrical cup and cuboid cup. The length of particles in the cup is AR = 5; H₀ and D₀ represent the penetration depth of impactor and diameter of impactor, respectively.