Impedance-Frequency Response of Closed Electrolytic Cells

Abstract

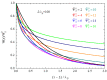
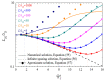
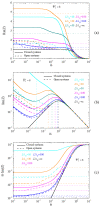
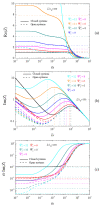
The electric AC response of electrolytic cells with DC bias is analyzed solving numerically the Poisson-Nernst-Planck equations and avoiding the commonly used infinite solution approximation. The results show the presence of an additional low-frequency dispersion process associated with the finite spacing of the electrodes. Moreover, we find that the condition of fixed ionic content inside the electrolytic cell has a strong bearing on both the steady-state and the frequency response. For example: the characteristic frequency of the high-frequency dispersion decreases when the DC potential increases and/or the electrode spacing decreases in the closed cell case, while it remains essentially insensitive on these changes for open cells. Finally, approximate analytic expressions for the dependences of the main parameters of both dispersion processes are also presented.

Keywords: Poisson-Nernst Planck equations; closed electrolytic cells; electrical impedance spectroscopy.

Figure 1

Ionic concentration at the central plane of closed electrolytic cells as function of the surface potential for the indicated $L/{\lambda }_D$ values.

Figure 2

Numerical results for the electric potential profiles in a closed electrolytic cell calculated for $L/{\lambda }_D=100$ and the indicated surface potential values.

Figure 3

Dependence of the electric double layer thickness values on the surface potential, calculated for the indicated $L/{\lambda }_D$ values. Vertical dot lines show surface potential values corresponding to the double layer thickness minima, Equation (58).

Figure 4

Spectra of the real part of the impedance (a), its imaginary part (b), and its imaginary part multiplied by the angular frequency (c), calculated for the indicated $L/{\lambda }_D$ values and the dimensionless surface potential ${\overline{\mathsf{\Psi }}}_S^0=8$. Dot and dash-dot straight lines (closed and open cells, respectively) correspond to the following: (a) Real part of the impedance at frequencies between both dispersions, Equation (61) for open or (62) for closed cells; (b) characteristic frequency of the high-frequency dispersion, Equation (60) for closed cells; (c) Low-frequency limit of the imaginary part of the impedance multiplied by the frequency, Equations (63), (64), and (25) for closed or Equation (28) for open cells.

Figure 5

Spectra of the real part of the impedance (a), the imaginary part (b), and the imaginary part multiplied by the angular frequency (c), calculated for the indicated dimensionless surface potential values and for $L/{\lambda }_D=100$. Dot and dash-dot straight lines (closed and open cells respectively) correspond to the following: (a) Real part of the impedance at frequencies between both dispersions, Equation (61) for open or (62) for closed cells; (b) characteristic frequency of the high-frequency dispersion, Equation (60) for closed cells; (c) low-frequency limit of the imaginary part of the impedance multiplied by the frequency, Equations (63), (64), and (25) for closed or Equation (28) for open cells.