Modeling human observer detection in undersampled magnetic resonance imaging reconstruction with total variation and wavelet sparsity regularization

Abstract

Purpose: Task-based assessment of image quality in undersampled magnetic resonance imaging provides a way of evaluating the impact of regularization on task performance. In this work, we evaluated the effect of total variation (TV) and wavelet regularization on human detection of signals with a varying background and validated a model observer in predicting human performance.

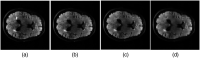
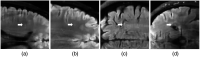
Approach: Human observer studies used two-alternative forced choice (2-AFC) trials with a small signal known exactly task but with varying backgrounds for fluid-attenuated inversion recovery images reconstructed from undersampled multi-coil data. We used a 3.48 undersampling factor with TV and a wavelet sparsity constraints. The sparse difference-of-Gaussians (S-DOG) observer with internal noise was used to model human observer detection. The internal noise for the S-DOG was chosen to match the average percent correct (PC) in 2-AFC studies for four observers using no regularization. That S-DOG model was used to predict the PC of human observers for a range of regularization parameters.

Results: We observed a trend that the human observer detection performance remained fairly constant for a broad range of values in the regularization parameter before decreasing at large values. A similar result was found for the normalized ensemble root mean squared error. Without changing the internal noise, the model observer tracked the performance of the human observers as the regularization was increased but overestimated the PC for large amounts of regularization for TV and wavelet sparsity, as well as the combination of both parameters.

Conclusions: For the task we studied, the S-DOG observer was able to reasonably predict human performance with both TV and wavelet sparsity regularizers over a broad range of regularization parameters. We observed a trend that task performance remained fairly constant for a range of regularization parameters before decreasing for large amounts of regularization.

Keywords: constrained reconstruction; image quality assessment; magnetic resonance imaging; model observers.

Fig. 1

(a) Sampling mask for 4× undersampling, (b) fully sampled image, and (c) undersampled constrained reconstruction with no TV regularization, aliasing in the vertical axis is visible in the undersampled image. The acquisition had a 2× oversampling in the horizonal direction.

Fig. 2

Sample undersampled images reconstructed with TV regularization, (a) ${\alpha }_{\mathrm{TV}}=0.01$, (b) ${\alpha }_{\mathrm{TV}}=0.02$, (c) ${\alpha }_{\mathrm{TV}}=0.05$, and (d) ${\alpha }_{\mathrm{TV}}=0.1$. As the regularization increases, there are reduced aliasing artifacts but also reduced resolution. The arrow in panel (a) shows the location of one of the undersampling artifacts.

Fig. 3

Sample undersampled images reconstructed with wavelet sparsity: (a) ${\alpha }_W=0.01$, (b) ${\alpha }_W=0.02$, (c) ${\alpha }_W=0.05$, and (d) ${\alpha }_W=0.1$. As the regularization increases, there are reduced aliasing artifacts but also reduced resolution but with different texture than in TV regularization. The arrow in image A shows the location of one of the undersampling artifacts.

Fig. 4

Sample 2AFC trial with signal in the left image. The arrow present in this image was not used in the observer study and is there to help the reader identify the signal. In order to see differences in performances due to regularization, the images used were subtle. These images were generated with no regularization but the artifacts are more visible in the image to the right.

Fig. 5

(a) The cross section of S-DOG channels matched for human performance with no TV regularization in the frequency domain and (b) spatial domain.

Fig. 6

(a) S-DOG observer with internal noise matched to average human observer for images with no TV regularization. The S-DOG observer tracked the human observer data for the other regularization parameters. The S-DOG slightly overestimates for the largest regularization parameters. (b) Normalized ERMSE for varying TV regularization. The ERMSE metric leads to similar conclusions as the 2-AFC detection performance.

Fig. 7

(a) S-DOG observer with internal noise matched to average human observer for images with no wavelet sparsity. The S-DOG observer tracked the human observer data for the other regularization parameters. The S-DOG slightly overestimates for the largest regularization parameter. (b) Normalized ERMSE for varying wavelet sparsity. The ERMSE metric leads to similar conclusions as the 2-AFC detection performance.

Fig. 8

(a) The S-DOG observer predicts that even with a combination of wavelet and TV regularization, the average human observer performance remains fairly constant for this task for a range of regularization parameters and that it degrades at high levels of regularization. (b) The ERMSE behaves leads to similar conclusions as the S-DOG observer.

Fig. 9

(a) The S-DOG observer predicts that even with a combination of wavelet and TV regularization, the average human observer performance remains fairly constant for this task for a range of regularization parameters and that it degrades at high levels of regularization. (b) The ERMSE behaves leads to similar conclusions as the S-DOG observer.

Fig. 10

Sample subimages with lesions undersampled images reconstructed with TV and wavelet regularization, (a) ${\alpha }_{\mathrm{TV}}=0.0$, ${\alpha }_W=0.0$, (b) ${\alpha }_{\mathrm{TV}}=0.01$, ${\alpha }_W=0.01$, (c) ${\alpha }_{\mathrm{TV}}=0.02$, ${\alpha }_W=0.02$, and (d) ${\alpha }_{\mathrm{TV}}=0.05$, ${\alpha }_W=0.05$. As the regularization increases, there are reduced aliasing artifacts but also reduced resolution. Image quality and task performance (as measured by the average PC shown in the images) is difficult to assess from the sample images.

Fig. 11

Sample subimages with lesions undersampled images reconstructed with TV and wavelet regularization (${\alpha }_{\mathrm{TV}}=0.01$, ${\alpha }_W=0.01$). Even though the signals are always present, subjectively we see that the signal is easier to detect in panels (a) and (b) but harder to see in panels (c) and (d). This variability in visibility due to background variability for the same reconstruction is one of the reasons why it is important to average over multiple backgrounds to estimate performance.