Dynamic tilting in perovskites

Abstract

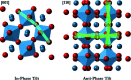
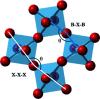
A new computational analysis of tilt behaviour in perovskites is presented. This includes the development of a computational program - PALAMEDES - to extract tilt angles and the tilt phase from molecular dynamics simulations. The results are used to generate simulated selected-area electron and neutron diffraction patterns which are compared with experimental patterns for CaTiO₃. The simulations not only reproduced all symmetrically allowed superlattice reflections associated with tilt but also showed local correlations that give rise to symmetrically forbidden reflections and the kinematic origin of diffuse scattering.

Keywords: diffraction; molecular dynamics; perovskites; superlattice; tilt.

Figure 1

Comparison of the untilted and tilted structures of BaTiO₃ (left) and CaTiO₃ (right). Red, oxygen; light blue, Ti; green, Ba; dark blue, Ca ions (CrystalMaker, 2018 ▸).

Figure 2

Comparison of tilting in a perovskite. Each image involves two layers of octahedra to demonstrate that each can tilt by the same magnitude, but either in the same direction or in the opposite direction, giving in-phase or anti-phase tilting, respectively.

Figure 3

We define tilt angle as the angle between the connected vectors, [XX]₁ and [XX]₂, in an ABX ₃ perovskite. Vectors [XX]₁, [XX]₂ run from one corner of an octahedron to the opposite corner, crossing near the centroid of the octahedron. This is compared with the angle between vectors [BX]₃ and [XB]₄.

Figure 4

The definition of tilt within a perovskite, based upon the geometric connectivity of the atoms. In (a) we define the cube made by the B-site ions. In (b) we define two edges of the cube (B _1b B _1a , B _2b B _2a ), their midpoints (M ₁, M ₂), and then vectors between these midpoints and both the B sites (M ₁ B _1b , M ₁ B _1a , M ₂ B _2b , M ₂ B _2a ) and the X (M ₁ X ₁, M ₂ X ₂). In (c) the midpoints are connected by a vector (M ₁ M ₂), which allows us to define the ‘torsional’ angles (X ₁ M ₁ M ₂ X ₂, X ₁ M ₁ M ₂ B _2a , X ₁ M ₁ M ₂ B _2b , B _1a M ₁ M ₂ X ₂, B _1b M ₁ M ₂X₂). We define the ‘torsional’ angle X ₁ M ₁ M ₂ X ₂ as follows. Looking in the direction M ₁ M ₂, the ‘torsional’ angle is the clockwise angle through which it is necessary to rotate the line X ₁ M ₁ such that the planes X ₁ M ₁ M ₂ and M ₁ M ₂ X ₂ are superimposed. The other ‘torsional’ angles are defined analogously. The system shows in-phase tilt if X ₂ M ₂ M ₁ X ₁ < min(X ₁ M ₁ M ₂ B _2a , X ₁ M ₁ M ₂ B _2b , B _1a M ₁ M ₂ X ₂, B _1b M ₁ M ₂ X ₂) as noted in (d).

Figure 5

Simulated pattern from a single molecular dynamics (SMD) configuration, simulated pattern from 1000 averaged (AV) configurations (see Section 3) and experimental (EXP) selected-area patterns from CaTiO₃ indexed in a pseudo-cubic setting. a = anti-phase, i = in-phase, c = cation shift and f = forbidden reflections (by symmetry and discounting double diffraction). Experimental data from Woodward & Reaney (2005 ▸).

Figure 6

Time-of-flight neutron diffractogram for the CaTiO₃ system at 50 K. Top: experimental pattern (using data from Knight, 2011 ▸). Bottom: simulated pattern obtained from molecular dynamics trajectories using Crystal Diffract from the CrystalMaker code suite (CrystalMaker, 2021a ▸).